Wiązka zadań
Tonące drewno
Prezentowane zadanie pochodzi z zestawu zadań badania Pracowni Przedmiotów Przyrodniczych „Laboratorium myślenia”. Wszelkie informacje dotyczące badania „Laboratorium myślenia” dostępne są na stronie eduentuzjasci.pl.
Zadanie
Drewno uważane jest za materiał tak lekki, że zawsze unosi się na wodzie. Tymczasem niektóre gatunki drewna mają tak dużą gęstość – zwłaszcza, gdy nie są do końca wysuszone – że mogą tonąć.
Do wody zaczerpniętej z Adriatyku wrzucono trzy kawałki drewna: dębowego o gęstości 1025 kg/m3, drewna z eukaliptusa – o gęstości 1035 kg/m3 oraz hebanu o gęstości 1100 kg/m3. Okazało się, że tylko kawałek drewna dębowego unosił się na powierzchni, pozostałe zaś utonęły.
Poniższy wykres przedstawia zależność gęstości wody od jej zasolenia.
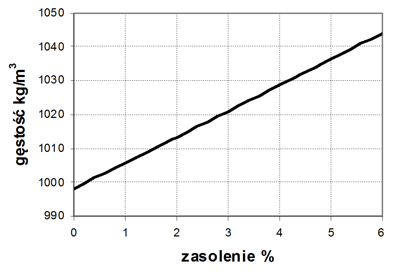
Korzystając z powyższych informacji, można oszacować, że zasolenie wody w Adriatyku wynosi
`square` A. około 2%
`square` B. około 4%
`square` C. około 6%
`square` D. powyżej 6%
Poprawna odpowiedź
B
Wymaganie ogólne
4 Posługiwanie się informacjami pochodzącymi z analizy przeczytanych tekstów (w tym popularno-naukowych).
Wymaganie szczegółowe
3.8. Właściwości materii. Uczeń analizuje i porównuje wartości sił wyporu dla ciał zanurzonych w cieczy lub gazie
3.9. Właściwości materii. Uczeń wyjaśnia pływanie ciał na podstawie prawa Archimedesa.
8.7. Wymagania przekrojowe. Uczeń rozpoznaje proporcjonalność prostą na podstawie danych liczbowych lub na podstawie wykresu oraz posługuje się proporcjonalnością prostą
8.8. Wymagania przekrojowe. Uczeń sporządza wykres na podstawie danych z tabeli (oznaczenie wielkości i skali na osiach) a także odczytuje dane z wykresu
Komentarz
Zadanie nadaje się do wykorzystania na lekcji, jak również jako zadanie domowe, które należy sprawdzić i omówić w klasie. Podane w nim informacje są prawdziwe i opisują doświadczenie znane uczniom - pływanie drewna w wodzie. Jest to jednak drewno o nietypowych – dużych gęstościach.
Zadanie nie jest łatwe – wymaga bowiem kolejno:
- odszukania potrzebnych informacji w tekście,
- odczytania z wykresu granicznych poziomów zasolenia dla gęstości poszczególnych gatunków drewna,
- ustalenia, który przedział między odnalezionymi wynikami zawiera właściwą odpowiedź.
W zadaniu badano umiejętność połączenia ze sobą: wiedzy (o pływaniu ciał), informacji odczytanych z tekstu (dane o gęstości ciał) oraz danych z wykresu (odczytanie zależności).
Dodatkowym utrudnieniem był fakt, że żądano oszacowania, a nie odczytania z wykresu konkretnej wartości.
Teoretycznie uczeń z lekcji fizyki powinien wiedzieć jedynie, iż warunkiem pływania jednorodnych ciał w wodzie jest ich gęstość mniejsza od gęstości wody. Równie ważne jest jednak, aby uczeń wynosił z lekcji również np. umiejętność przeprowadzenia logicznego wnioskowania na podstawie przedstawionych mu informacji.
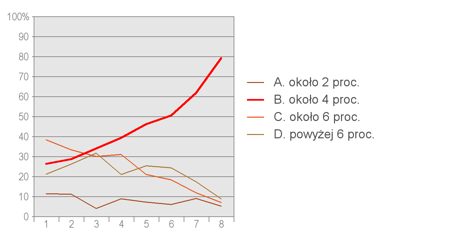
Poniżej pokazano wyniki badania wykonanego na losowej próbie około 5000 uczniów klas I szkół ponadgimnazjalnych. Badaną populację podzielono według uzyskanych wyników na osiem równolicznych grup, nadając im numery od 1 do 8 (1 – uczniowie najsłabsi, 8 – najlepsi).
Liczby 1-8 na poziomej osi oznaczają numer grupy, a liczby na pionowej osi – procent uczniów z danej grupy, jaki wybrał daną odpowiedź.
Wykres poniżej przedstawia ilość poprawnych i niepoprawnych odpowiedzi uczniów.
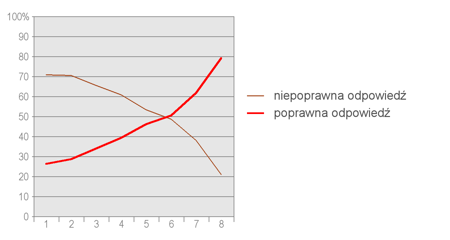
Zadanie okazało się niezwykle trudne dla uczniów słabych, natomiast stosunkowo łatwe dla dobrych. W najwyższej grupie aż 80% uczniów udzieliło poprawnej odpowiedzi, natomiast w najsłabszej wynik pozostawał na poziomie przypadkowego trafienia.
Zadanie było nietypowe, gdyż wymagało znalezienia odpowiedniego przedziału wartości zasolenia wody, a nie tylko prostego odczytania jej z wykresu.
Jak widać, lepsi uczniowie potrafią sobie radzić nawet z dość skomplikowanym procesem myślowym. Być może jakiś wpływ na to miał fakt, że w zadaniu nie wystąpiła konieczność wykorzystania wzorów, obliczeń, definicji oraz mało intuicyjnych pojęć.
W tym kontekście uzyskane wyniki napawają ostrożnym optymizmem, choć z drugiej strony oczekiwalibyśmy, że większy odsetek uczniów poradzi sobie dobrze z podobnymi zagadnieniami.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





