Wiązka zadań
Zagęszczenie mniszków
Zadanie
Uczniowie badali zagęszczenie mniszka lekarskiego w pasie zieleni wzdłuż ulicy Dmuchawcowej. Podzielili się w tym celu na 3 zespoły, z których każdy badał losowo wybrany trawnik pomiędzy dwiema przecznicami (rysunek). Zespół I znalazł 23 osobniki mniszka, zespół II – 38, a zespół III – 15 osobników.
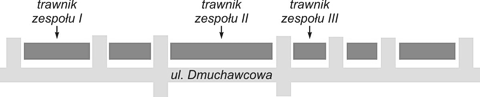
Na podstawie tych danych uczniowie nie byli jednak w stanie określić średniego zagęszczenia mniszka wzdłuż całej ulicy Dmuchawcowej. Było tak ponieważ:
`square` A. nie zmierzyli powierzchni trawników, na których liczyli mniszki.
`square` B. nie policzyli wszystkich mniszków rosnących wzdłuż całej ul. Dmuchawcowej.
`square` C. uzyskali wyniki zbyt zróżnicowane, aby można było obliczyć wartość średnią.
`square` D. nie zmierzyli całkowitej powierzchni wszystkich trawników wzdłuż ul. Dmuchawcowej.
Poprawna odpowiedź
A
Wymaganie ogólne
2.1 Znajomość metodyki badań biologicznych. Uczeń planuje, przeprowadza i dokumentuje obserwacje i proste doświadczenia biologiczne.
Wymaganie szczegółowe
Komentarz
Zadanie to odnosi się bezpośrednio do jednej z obserwacji zalecanych w podstawie programowej – określania zagęszczenia wybranego gatunku rośliny zielnej. Aby poprawnie je rozwiązać, uczniowie powinni rozumieć, że dla oszacowania średniego zagęszczenia na danym obszarze (pasie zieleni wzdłuż całej ulicy) nie jest konieczne zliczenie wszystkich rosnących tam roślin – wystarczy przeprowadzić pomiary dla kilku prób losowych (trawników). Muszą także wiedzieć, że zagęszczenie obliczamy dzieląc liczbę osobników przez pole powierzchni terenu, na którym je znaleziono (trawnika). Uczniowie, którzy przeprowadzili ze zrozumieniem zalecaną w podstawie programowej obserwację, nie powinni mieć zatem większych trudności z poprawnym rozwiązaniem tego zadania. Już sama znajomość sposobu obliczania zagęszczenia danego gatunku powinna skłonić ich do wyboru odpowiedzi A – nie można bowiem ustalić zagęszczenia rośliny bez znajomości powierzchni badanego obszaru. Pozostałe odpowiedzi można natomiast odrzucić na podstawie wiedzy o szacowaniu wartości średniej w oparciu o wyniki dla kilku prób losowych. Nie jest wówczas konieczna znajomość powierzchni wszystkich trawników wzdłuż ulicy (odpowiedź D) ani łącznej liczby rosnących na nich mniszków (odpowiedź B). Wystarczy bowiem obliczyć wartość średnią z wyników uzyskanych dla trzech wylosowanych trawników, a różnice między nimi nie uniemożliwiają przeprowadzenia tych obliczeń (odpowiedź C). Warto również zauważyć, że wyniki uczniów mówią tylko o różnej liczebności mniszka na poszczególnych trawnikach – jeśli natomiast weźmie się pod uwagę ich powierzchnie (przedstawione w przybliżony sposób na rysunku) można przypuszczać, że zagęszczenie jest we wszystkich trzech wypadkach porównywalne.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl