Wiązka zadań
Dźwignia
Zadanie
Jacek i Mirek przenoszą razem słupek o długości 4 m. Jacek narzeka, że niesie mu się bardzo ciężko, a Mirek uważa, że nie jest tak źle. Chłopcy zastanawiają, się co może być przyczyną różnicy ich odczuć. Mirkowi przypomina się lekcja fizyki o dźwigni dwustronnej. Zaczyna podejrzewać, że przyczyną narzekań Jacka jest fakt, że nie trzyma on słupka za sam koniec.
Istotnie, taki układ jest nieco podobny do dźwigni dwustronnej, a jej zasadę równowagi można tu też zastosować, jeżeli za oś obrotu dźwigni przyjmiemy środek ciężkości słupka, znajdujący się w środku jego długości. Suma sił, z jakimi działają obaj chłopcy, musi być przy tym równa ciężarowi słupka.
Na rysunku pokazano siły, z jakimi chłopcy działają na słupek.
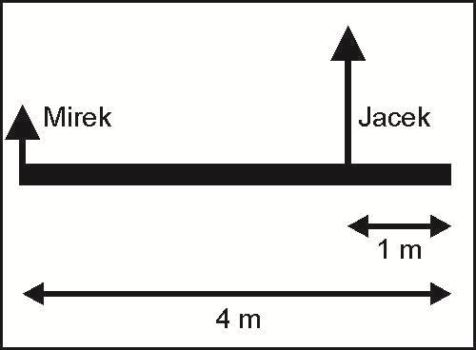
Korzystając z powyższych informacji, można obliczyć, że na Mirka przypada:
`square` A. połowa ciężaru słupka
`square` B. 1/3 ciężaru słupka
`square` C. 1/4 ciężaru słupka
`square` D. 2/3 ciężaru słupka
Poprawna odpowiedź
B
Wymaganie ogólne
3 Wskazywanie w otaczającej rzeczywistości przykładów zjawisk opisywanych za pomocą poznanych praw i zależności fizycznych.
Wymaganie szczegółowe
1.11. Ruch prostoliniowy i siły. Uczeń wyjaśnia zasadę działania dźwigni dwustronnej, bloku nieruchomego, kołowrotu
Komentarz
Zadanie sprawdza umiejętność wykorzystania wiedzy z fizyki w konkretnej sytuacji życiowej. Dotyczy zasad działania dźwigni dwustronnej. Zadanie jest bardzo trudne, bo nietypowe. W opisanym doświadczeniu z przenoszeniem słupka, nie widać dźwigni tak wyraźnie, jak np. przy huśtawce. Trzeba ją sobie wyobrazić.
Można przeprowadzić proste doświadczenie: uczeń chwyta za słupek w środku ciężkości, wówczas końca nie trzeba podtrzymywać. Gdy złapie nieco z boku – koniec słupka opada na podłogę. Wystarczy jednak niewielka siła aby go utrzymać w poziomie. Drugi uczeń musi nieco podtrzymać koniec słupka. Im bliżej końca słupka przesuwa się pierwszy uczeń, tym większą siłą musi działać drugi, aby utrzymać słupek w poziomie. Po takim doświadczeniu uczniowie powinni bez wahania, niejako intuicyjnie wiedzieć, że Jacek będzie musiał działać większą siłą niż Mirek.
Przeanalizujmy rysunek do zadania. Ponieważ Jacek podtrzymuje klocek w odległości dwukrotnie mniejszej od środka ciężkości niż Mirek, to musi dźwigać ciężar dwukrotnie większy niż kolega. Zasada dźwigni: dwa razy dłuższe ramię, to dwa razy mniejsza siła. Skoro razem muszą unieść cały słupek, to suma ich sił musi się równać ciężarowi słupka. Nasuwa się tutaj pytanie: jak podzielić ciężar klocka między nimi, aby jeden dźwigał dwa razy więcej niż drugi? Zakładamy, że jeśli Mirek dźwiga jedną część, to Jacek musi dźwigać dwie takie same części klocka. Stąd wniosek, że klocek należy podzielić na trzy jednakowe części i jedną część (1/3całości) przydzielić jednemu chłopcu, a dwie części (2/3 całości) drugiemu. Wynika z tego, że Mirek dźwiga 1/3 ciężaru słupka a Jacek 2/3 tego ciężaru. Odpowiedź B.
Spośród wszystkich uczniów pierwszych klas liceów ogólnokształcących biorących udział w badaniu pilotażowym około 28% rozwiązało zadanie prawidłowo. Równie często (ok. 24% wszystkich badanych) uczniowie dochodzili do błędnego wniosku, że na Mirka przypada 2/3 ciężaru, czyli więcej niż na Jacka, co jest o tyle zadziwiające, że z treści zadania wyraźnie wynika, że bardziej obciążony jest Jacek. Natomiast najczęściej wybierana była odpowiedź C (39%), przypisująca Mirkowi ¼ ciężaru do dźwigania. Widocznie największy problem sprawiło uczniom takie podzielenie ciężaru między chłopców, aby jeden niósł dwa razy tyle co drugi. Możliwe również, że uczniowie po prostu podzielili wartości podane na rysunku 1m/4m. Zadanie wyraźnie różnicowało uczniów.
Na podstawie analizy wyników, nasuwa się uwaga do nauczycieli, aby po rozwiązaniu przez uczniów zadania, zachęcali ich do przeczytania jego treści jeszcze raz, a następnie do skonfrontowania wybranej przez nich odpowiedzi z treścią zadania. Niech uczeń zastanowi się, czy wynik, który wskazał, pasuje logicznie do podanych w treści warunków.
Należy również zachęcać nauczycieli do aranżowania w klasie różnorakich prostych doświadczeń, w których uczniowie mogą sami ‘odczuć’ różnice sił i próbować wyciągać wnioski z sytuacji z życia codziennego.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





