Wiązka zadań
Paralaksa
Zadanie
Adam wykonał bardzo proste doświadczenie: koleżanka trzymała na wprost przed Adamem ołówek, a on spojrzał na niego raz lewym, a raz prawym okiem. Chłopiec zaobserwował, że na tle ściany ołówek znajdował się w dwóch różnych miejscach. Na poniższym rysunku zostały przedstawione miejsca, w których znajdowały się Adam i ołówek względem ściany.
W której sytuacji (A-D) Adam zauważy największą zmianę położenia ołówka przy obserwacji raz prawym, a raz lewym okiem? Zaznacz prawidłową odpowiedź.
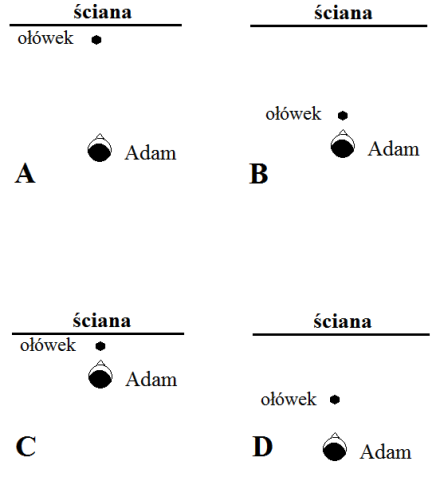
Adam zauważy największą zmianę położenia ołówka w przypadku przedstawionym na rysunku:
`square` A.
`square` B.
`square` C.
`square` D.
Poprawna odpowiedź
B
Wymaganie ogólne
Wymaganie szczegółowe
Komentarz
Ze zjawiskiem paralaksy spotykamy się nie tylko w astronomii, ale również w życiu codziennym. Na przykład jadąc pociągiem obserwujemy, że na tle odległego krajobrazu różne przedmioty (słupy, drzewa, budynki) przesuwają się z różną prędkością, w zależności od ich umiejscowienia pomiędzy obserwatorem a nieruchomym tłem. Między innymi możemy zauważyć, że słupy trakcyjne przesuwają się dosyć wyraźnie na tle odległych wzgórz lub lasów. Wynika z tego, że najszybciej zmieniają położenie obiekty znajdujące się najbliżej obserwatora (a najdalej od tła). Innymi słowy, dla tych obiektów obserwowana paralaksa jest największa.
Prezentowane zadanie sprawdza umiejętność przewidywania wyniku doświadczenia, polegającego na tym, że obserwator patrzy na ołówek raz jednym, raz drugim okiem, przy kilku różnych kombinacjach odległości ołówka od obserwatora i obserwatora od ściany. Zadaniem ucznia jest wskazanie sytuacji, w której zaobserwujemy największą zmianę położenia ołówka na tle ściany. Tak naprawdę zadanie można rozwiązać bez znajomości pojęcia paralaksy. Wystarczy na każdym rysunku narysować prostą oko-ołówek, a następnie przedłużyć tę prostą do ściany, po czym powtórzyć tę czynność dla drugiego oka. Oczywiście nic nie stoi na przeszkodzie, aby uczeń sam wykonał opisane doświadczenie. Największą zmianę położenia ołówka zaobserwujemy w sytuacji, w której odległość między przecięciami prostych ze ścianą będzie największa. W tym przypadku będzie to rysunek B.
W badaniu zadanie zostało poprawnie rozwiązane przez 49,8% uczniów pierwszych klas liceów. Nieco mniej popularne były odpowiedzi A i C (po około 20%), a najrzadziej była wybierana odpowiedź D (9,7%). Prawdopodobnie znaczna część badanych osób zaznaczała odpowiedź losowo. Warto tutaj zauważyć, że preferowane były odpowiedzi z początku listy, co doprowadziło do pewnego paradoksu: rysunek D był wybierany najrzadziej, chociaż to właśnie w tej sytuacji zaobserwujemy większą zmianę położenia ołówka niż w sytuacjach przedstawionych na rysunkach A i C. Tak naprawdę trudno w tej sytuacji określić, ile z osób wybierających poprawną odpowiedź zrobiło to świadomie.
Ponieważ rozumienie pojęcia paralaksy jest niezbędne do opanowania niektórych zagadnień przewidzianych zapisami podstawy programowej, warto gruntownie wytłumaczyć uczniom znaczenie tego terminu oraz omówić konsekwencje zjawiska paralaksy na prostych przykładach z życia codziennego. Można wykorzystać prezentowane zadanie w celu wprowadzenia uczniów w temat, a następnie poprosić ich o wykonanie opisanego w zadaniu doświadczenia i porównać jego wynik z przewidywaniami uczniów. Z pewnością takie porównanie może stać się początkiem dyskusji ukierunkowanej na zagadnienia związane ściśle z astronomią.
Utwór powstał w ramach projektu "Badanie jakości i efektywności oraz instytucjonalizacja zaplecza badawczego” współfinansowanego przez Unię Europejską ze środków Europejskiego Funduszu Społecznego
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl




