Wiązka zadań
Średnia ze średniej
Zadanie 1
Oblicz średnią arytmetyczną zestawu liczb: 4, 5, 9.
Poprawna odpowiedź
6
Wymaganie ogólne
4. Użycie i tworzenie strategii. Uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
5. Rozumowanie i argumentacja. Uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
Wymaganie szczegółowe
9.4 Statystyka opisowa i wprowadzenie do rachunku prawdopodobieństwa. Uczeń wyznacza średnią arytmetyczną i medianę zestawu danych.
Komentarz
Zadanie 2
Oblicz średnie z każdych dwóch różnych liczb zestawu 4, 5, 9.
Poprawna odpowiedź
4,5; 6,5; 7
Wymaganie ogólne
4. Użycie i tworzenie strategii. Uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
5. Rozumowanie i argumentacja. Uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
Wymaganie szczegółowe
9.4 Statystyka opisowa i wprowadzenie do rachunku prawdopodobieństwa. Uczeń wyznacza średnią arytmetyczną i medianę zestawu danych.
Komentarz
Zadanie 3
Oblicz średnią liczb otrzymanych w punkcie 2.
Poprawna odpowiedź
6
Wymaganie ogólne
4. Użycie i tworzenie strategii. Uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
5. Rozumowanie i argumentacja. Uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
Wymaganie szczegółowe
9.4 Statystyka opisowa i wprowadzenie do rachunku prawdopodobieństwa. Uczeń wyznacza średnią arytmetyczną i medianę zestawu danych.
Komentarz
Zadanie 4
Porównaj średnią pierwszego i drugiego zestawu.
Poprawna odpowiedź
Są równe.
Wymaganie ogólne
4. Użycie i tworzenie strategii. Uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
5. Rozumowanie i argumentacja. Uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
Wymaganie szczegółowe
9.4 Statystyka opisowa i wprowadzenie do rachunku prawdopodobieństwa. Uczeń wyznacza średnią arytmetyczną i medianę zestawu danych.
Komentarz
Zadania 1-4 są próbą wzbudzenia ciekawości poznawczej – czy zaobserwowana zbieżność wyników jest przypadkowa, czy jest w tym jakaś głębsza prawidłowość. Część uczniów z pewnością zechce sprawdzić to na innym zestawie liczb. Gdy znów wyniki okażą się takie same – być może zaczną szukać uogólnień i posłużą się algebrą.
Zadanie 5
Uzasadnij, że gdy dane są trzy różne liczby, to zestaw nowych liczb otrzymany w sposób opisany w zad. 1-4 ma taką samą średnią, jak zestaw początkowy.
Poprawna odpowiedź
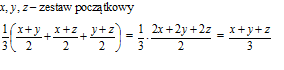
Wymaganie ogólne
4. Użycie i tworzenie strategii. Uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
5. Rozumowanie i argumentacja. Uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
Wymaganie szczegółowe
9.4 Statystyka opisowa i wprowadzenie do rachunku prawdopodobieństwa. Uczeń wyznacza średnią arytmetyczną i medianę zestawu danych.
Komentarz
Zadania 1-4 są próbą wzbudzenia ciekawości poznawczej – czy zaobserwowana zbieżność wyników jest przypadkowa, czy jest w tym jakaś głębsza prawidłowość. Część uczniów z pewnością zechce sprawdzić to na innym zestawie liczb. Gdy znów wyniki okażą się takie same – być może zaczną szukać uogólnień i posłużą się algebrą.
Zadanie zawiera elementy modelowania sytuacji, przy czym ta czynność wykorzystywana jest tu po to, aby pokazać że modele dwóch różnych procesów są de facto takie same. W rozwiązaniu tego zadania można znaleźć również stosowanie strategii i prowadzenie rozumowania. Dlatego jest to bardzo dobre zadanie służące rozwijaniu bardziej złożonych procesów intelektualnych.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





