Wiązka zadań
Równoległobok z trójkątem
Zadanie
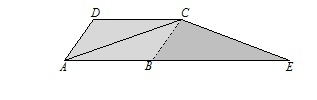
Pole równoległoboku ABCD jest równe 7. Do tego równoległoboku na przedłużeniu boku AB dobudowano trójkąt BEC tak, jak pokazano na rysunku. Oceń prawdziwość zdań (zamaluj kwadracik przy wybranej przez Ciebie odpowiedzi).
| I. | Jeżeli odcinki AB i BE mają równe długości, to pole trójkąta BEC jest równe 3,5. |
□ PRAWDA □ FAŁSZ |
| II. | Jeżeli odcinki AB i BE mają równe długości, to pola równoległoboku ABCD i trójkąta AEC będą równe. |
□ PRAWDA □ FAŁSZ |
| III. | Jeżeli odcinek BE będzie 2 razy dłuższy niż AB, to pola równoległoboku ABCD i trójkąta BEC będą równe. |
□ PRAWDA □ FAŁSZ |
| IV. | Jeśli odcinek BE będzie 7 razy dłuższy niż AB, to pole trójkąta AEC będzie równe 14. |
□ PRAWDA □ FAŁSZ |
Poprawna odpowiedź
I. P, II. P, III. P, IV. F
Wymaganie ogólne
5. Rozumowanie i argumentacja. Uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
Wymaganie szczegółowe
10.9 Figury płaskie. Uczeń oblicza pola i obwody trójkątów i czworokątów.
Komentarz
Jak zmienia się jedna wielkość geometryczna, gdy zmienia się inna? Takiego stawiania problemów geometrycznych (i rozwiązywania ich) uczy to zadanie. Zadanie może być zadaniem egzaminacyjnym, ale jest też dobrym narzędziem do pracy na lekcji. Jeśli uczniowie będą mieli z nim kłopoty, można zasugerować zrobienie rysunku do każdego z czterech rozważanych zdań, zgodne z podanymi wymiarami (czasem trzeba będzie uczniom pomóc w ustaleniu tych wymiarów). Potem można przejść do rozważenia, jak może się zmieniać omawiany wielokąt przy zachowaniu warunków podanych w kolejnych zdaniach.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





