Wiązka zadań
Rozcięty kwadrat
Zadanie
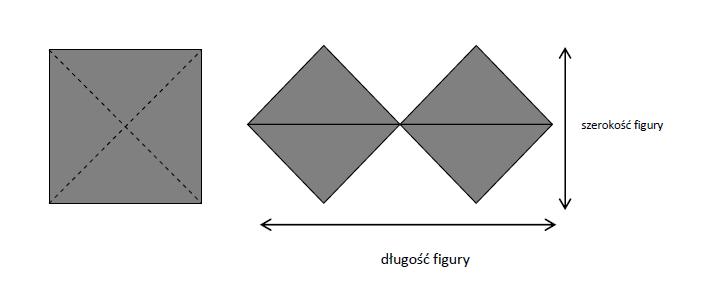
Kwadrat o boku 6 cm rozcięto wzdłuż przekątnych. Z otrzymanych trójkątów ułożono figurę złożoną z dwóch czworokątów tak, jak na rysunku. Na rysunku wyjaśniono również, co rozumiemy przez długość i szerokość otrzymanej figury. Pole tej figury to suma pól tworzących tę figurę czworokątów.
Oceń prawdziwość zdań (zamaluj kwadracik przy słowie PRAWDA lub FAŁSZ).
| 1. | Długość figury jest równa 12 cm. |
|
|
2. |
Szerokość figury jest równa `6sqrt(2)` cm. | |
|
3. |
Pole figury jest równe 36 cm2. | |
Poprawna odpowiedź
1. PRAWDA
2. FAŁSZ
3. PRAWDA
Wymaganie ogólne
1. Wykorzystywanie i tworzenie informacji. Uczeń interpretuje i tworzy teksty o charakterze matematycznym, używa języka matematycznego do opisu rozumowania i uzyskanych wyników.
2. Wykorzystywanie i interpretowanie reprezentacji. Uczeń używa prostych, dobrze znanych obiektów matematycznych, interpretuje pojęcia matematyczne i operuje obiektami matematycznymi.
Wymaganie szczegółowe
10.9 Figury płaskie. Uczeń oblicza pola i obwody trójkątów i czworokątów.
Komentarz
Informacje w zadaniu podane są zarówno w tekście, jak i na rysunku. Taki zapis danych sprzyja rozwijaniu umiejętności czytania ze zrozumieniem tekstów matematycznych przedstawionych w różnej formie i skłania uczniów do właściwego ich interpretowania. W zadaniu przedstawione są dwie figury, z których jedna powstała z drugiej. Uczeń musi zrozumieć przedstawioną sytuację, dostrzec zależności między obiema figurami i ich składowymi, a następnie wykorzystać znane zależności pomiędzy bokami i przekątnymi w kwadracie, co doskonale koresponduje z II. wymaganiem ogólnym podstawy, czyli z wykorzystywaniem i interpretowaniem reprezentacji.
Zadanie można modyfikować poprzez rozcinanie kwadratu w różny sposób, układanie z tych części różnych figur (np. podział kwadratu na trzy trójkąty i ułożenie z nich prostokąta) i badanie własności ułożonych figur. W następnym kroku można zamiast kwadratu rozcinać dowolną figurę o znanych uczniom własnościach. (Można w ten sposób przypomnieć uczniom, skąd wzięły się wzory na pola znanych im figur.) Takie działania sprzyjają kształtowaniu twórczej i otwartej postawy uczniów wobec różnych problemów matematycznych.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





