Wiązka zadań
Biegowe rekordy świata
Zadanie
Na wykresie przedstawiono dane dotyczące rekordów świata mężczyzn w biegach na dystansach od 200 m do 1500 m.
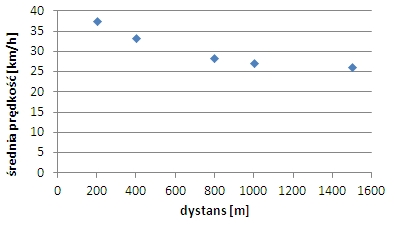
Dane za: http://en.wikipedia.org/wiki/Athletics_world_records
Którą z poniższych zależności ilustruje ten wykres?
`square` A. Im dłuższy dystans, tym więcej czasu zajmuje jego pokonanie.
`square` B. Im dłuższy dystans, tym wolniej zawodnik biegnie.
`square` C. Im wyższa prędkość zawodnika, tym szybciej pokonuje dystans.
`square` D. Im wyższa prędkość zawodnika, tym krótszy staje się dystans.
Poprawna odpowiedź
B
Wymaganie ogólne
1 Wykorzystanie wielkości fizycznych do opisu poznanych zjawisk lub rozwiązania prostych zadań obliczeniowych.
3 Wskazywanie w otaczającej rzeczywistości przykładów zjawisk opisywanych za pomocą poznanych praw i zależności fizycznych.
Wymaganie szczegółowe
8.9. Wymagania przekrojowe. Uczeń rozpoznaje zależność rosnącą i malejącą na podstawie danych z tabeli lub na podstawie wykresu oraz wskazuje wielkość maksymalną i minimalną
Komentarz
Zadanie nadaje się do wykorzystania na lekcji. Opisana w nim zależność nie jest wymyślona, ale przedstawia prawdziwe dane. Uczniowie nieraz w życiu będą mieli do czynienia z podobnymi wykresami, dotyczącymi różnych aspektów wiedzy. Tym ważniejsza jest umiejętność ich prawidłowej interpretacji.
Zadanie wydaje się na pierwszy rzut oka absolutnie banalne: wystarczy przecież odczytać opisy obu osi wykresu, aby wiedzieć, co on przedstawia. Trzeba jednak pamiętać o następujących faktach:
- czym innym dla ucznia jest sytuacja, w której osie są opisane jako x i y, a czym innym, kiedy są to konkretne wielkości fizyczne;
- opis typu „szybciej pokonuje dystans” wymaga interpretacji i w tym wypadku oznacza, że czas jest krótszy;
- do interpretacji wniosków z wykresu potrzebna jest pewna wprawa, której wielu nastolatków nie ma.
Wskutek tego zadanie, które wydaje się banalne, może sprawić uczniowi nie lada kłopot. Trudność potęguje fakt, że dystraktory zadania (z wyjątkiem ostatniego) są zdaniami prawdziwymi. Prawie wszystkie też operują opisanym na osiach wielkościami prędkości i dystansu. Jeżeli uczniowie rozwiązują to zadanie słabo, warto poświęcić mu więcej czasu i przedyskutować je na lekcji. Trzeba na początek uświadomić uczniom, że szukamy nie tyle jedynego prawdziwego zdania, ile zdania, które najlepiej opisuje zależność widoczną na wykresie. Następnie uczniowie powinni zastanowić się, jak mogą wyglądać wykresy odpowiadające zależnościom przedstawionym w dystraktorach.
- Wykres zależności A powinien mieć na pionowej osi bezpośrednio czas rekordów, a nie wyznaczoną z nich prędkość średnią. Byłaby to zależność rosnąca.
- Zdanie B opisuje zależność przedstawioną na wykresie, gdyż określenie „wolniej biegnie” oznacza mniejszą prędkość.
- Dystraktor C dotyczy wykresu opisującego jeden konkretny dystans. Na osi poziomej powinna znaleźć się prędkość, a na osi pionowej czas pokonania tego dystansu z tą prędkością. Byłaby to funkcja malejąca.
- Dystraktor D jest jedynym tu nieprawdziwym zdaniem. Dystans bowiem nie zależy od prędkości biegu. Niemniej jednak potocznie mówi się czasem: im szybciej biegniesz, tym cel wydaje się bliższy, co może zmylić niejednego ucznia.
Warto podkreślić, że w zadaniu nie chodzi o obliczenia lub szacunki. Celem zasadniczym jest umiejętność trafnego odczytania głównego przesłania, jakie niesie ze sobą przedstawiony wykres.
Można poprosić uczniów o wyszukanie w domu danych dotyczących rekordów świata na różnych dystansach, co będzie ciekawym rozwinięciem tematu. Na kolejnej lekcji można wówczas pokazać, że na pozór oczywista zależność przedstawiona w zadaniu nie jest do końca taka prosta. Okazuje się bowiem, że średnia prędkość biegaczy na dystansie 60 m oraz 100 m jest mniejsza niż na 200 m. Warto wywołać dyskusję, która – przy ewentualnej pomocy nauczyciela – powinna doprowadzić do wyjaśnienia tej rozbieżności. Przyczyną niezgodności wyników z biegów sprinterskich z tendencją opisaną wykresem w zadaniu jest bowiem start do biegu. Przy krótkich dystansach, strata związana z nim jest na tyle duża, że w znaczący sposób wpływa na średnią prędkość, jaką uzyskuje biegacz na całym dystansie. Na długich dystansach natomiast nie ma ona znaczenia. Jak widać, mamy więc dwa czynniki, które w różny sposób wpływają na średnią prędkość biegacza:
- straty spowodowane startem, czyli koniecznością rozpędzenia się, obniżają prędkość średnią tylko przy krótkich dystansach, na długich są do pominięcia;
- zmęczenie spowodowane biegiem również obniża prędkość średnią, ale na długich dystansach; na krótkich nie ma dużego znaczenia.
Gdyby istniał tylko czynnik pierwszy – wykres z zadania byłby funkcją rosnącą, gdyby zaś tylko drugi – byłby funkcją malejącą (jak w zadaniu). Nałożenie obu czynników na siebie powoduje, że powstaje wykres będący ich połączeniem.
Jak się okazuje, istnieje jeszcze jeden istotny aspekt wpływający na prędkość średnią biegaczy. Jest on określony przez dwie liczby: początkowy zapas energii biegacza i tempo jej pozyskiwania w czasie biegu. W podręczniku „Fizyka dla przyrodników” (Kane, Sternheim, PWN, Warszawa 1988) podano niezwykle ciekawy model matematyczny opisujący ten problem w sposób zrozumiały nawet dla gimnazjalisty. Przytoczymy tu tylko część opisanego tam rozumowania. Zgodnie z nim sportowiec-biegacz na starcie dysponuje energią w ilości około 193 kJ, natomiast tempo, w jakim potrafi pozyskiwać w trakcie biegu energię z przemian metabolicznych, wynosi około 3,3 kW. Wskutek tego sprinterzy dystans 100 m pokonują w całości wyłącznie dzięki zgromadzonej i gotowej do wykorzystania energii, zużywając jej przy tym około 94 kJ. W porównaniu bowiem do zapasu 193 kJ energia, jaką może uzyskać sprinter w czasie 10 sekund biegu na 100 m, wynosi zaledwie 33 kJ. Na długim dystansie sytuacja się odwraca. Pokonanie dystansu 5 km wymaga energii około 2820 kJ, dlatego główną rolę gra jej pozyskiwanie w czasie biegu – początkowy zapas jest znikomo mały w porównaniu z zapotrzebowaniem.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





