Wiązka zadań
Huśtawka
Zadanie
Podczas niedzielnego wyjścia do parku Ania namówiła tatę, aby pobawił się na huśtawce razem z nią i jej koleżanką Basią. W trakcie zabawy tacie i dziewczynkom udało się usadowić na huśtawce tak, aby była ona w równowadze (patrz rys poniżej).
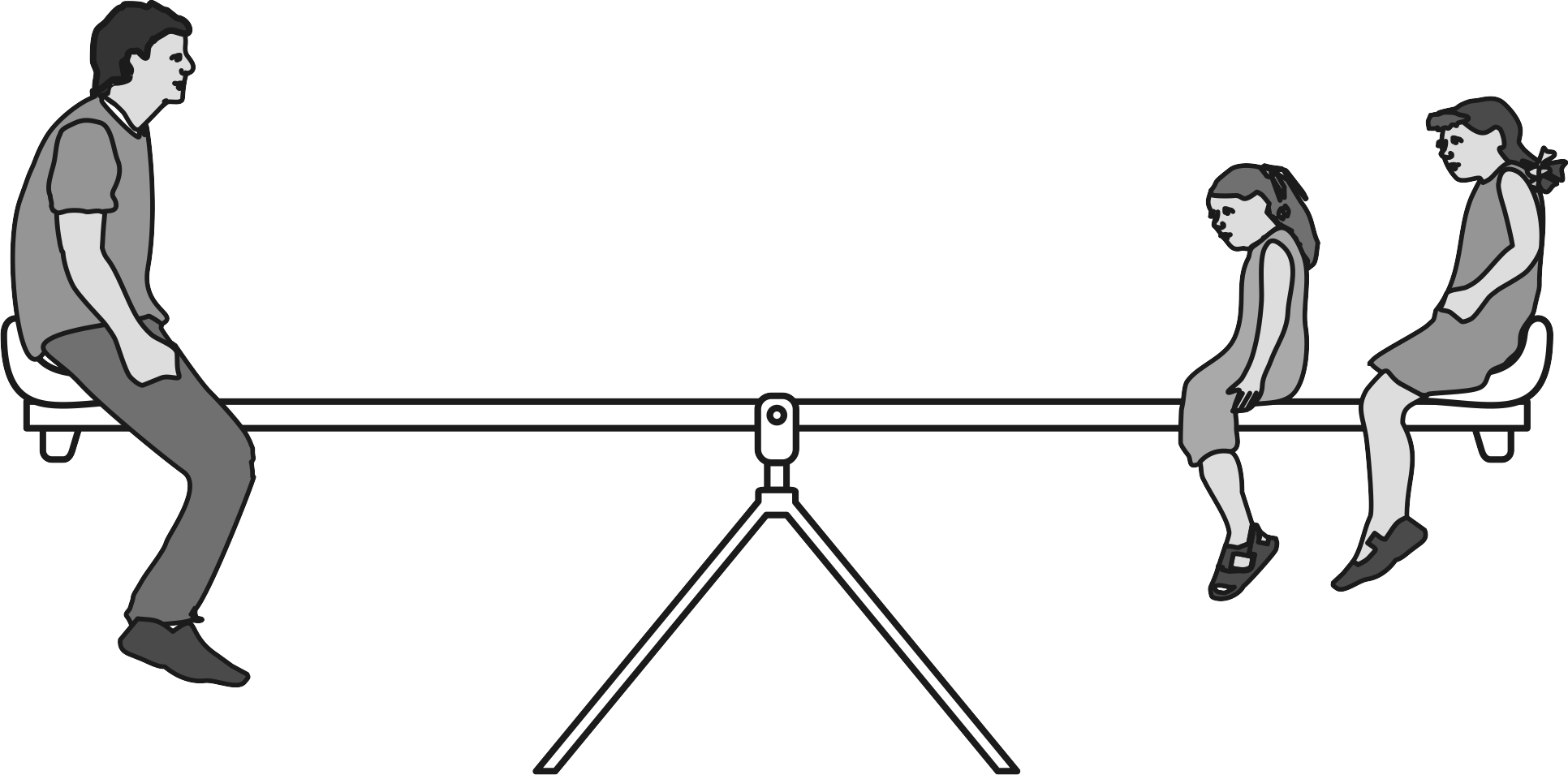
Zaznacz, które z niżej wymienionych stwierdzeń można wysnuć wyłącznie na podstawie obserwacji sytuacji pokazanej na rysunku.
| Stwierdzenia | tak czy nie? |
| 1. Tata jest cięższy od Basi. | `square` tak / `square` nie |
| 2. Ania waży nieco więcej niż Basia. | `square` tak / `square` nie |
| 3. Ania i Basia ważą razem nieco więcej niż tata. | `square` tak / `square` nie |
Poprawna odpowiedź
1.Tak., 2.Nie., 3.Tak.
Wymaganie ogólne
3 Wskazywanie w otaczającej rzeczywistości przykładów zjawisk opisywanych za pomocą poznanych praw i zależności fizycznych.
Wymaganie szczegółowe
1.11. Ruch prostoliniowy i siły. Uczeń wyjaśnia zasadę działania dźwigni dwustronnej, bloku nieruchomego, kołowrotu
Komentarz
Zadanie sprawdza umiejętność wykorzystania wiedzy z fizyki w konkretnej sytuacji życiowej. Huśtawka jest typowym przykładem dźwigni dwustronnej i zasady pracy tej dźwigni mają praktyczne zastosowanie w trakcie zabawy na huśtawce.
Przeanalizujmy rysunek do zadania, opierając się na prawie równowagi dźwigni dwustronnej. Na podstawie analizy tekstu wnioskujemy, ze wszystkie trzy osoby metodą prób i błędów wybrały dla siebie takie miejsca, aby huśtawka z ludźmi przyjęła pozycję poziomą i pozostała w równowadze. Zatem na podstawie prawa równowagi dźwigni, iloczyny działających po obu stronach sił i ich ramion są równe. W tym wypadku siłami są ciężary osób siedzących na huśtawce, a ramionami są odległości tych osób od środka huśtawki (od osi obrotu dźwigni). Tata siedzi po jednej stronie huśtawki, a dwie dziewczynki po jej drugiej stronie, przy czym odległość taty od środka huśtawki jest taka sama jak odległość jednej z dziewczynek i trochę większa niż odległość drugiej dziewczynki od środka huśtawki. Tato swoim ciężarem z jednej strony dźwigni równoważy ciężary obu dziewczynek po drugiej stronie. Zatem ciężar taty musi być większy od ciężaru którejkolwiek z dziewczynek, zarówno Ani jak i Basi. Prawdziwe stwierdzenie nr 1. Gdyby dziewczynki razem ważyły dokładnie tyle samo, co tata, to obydwie musiałyby siedzieć na samym końcu (w tej samej odległości od środka huśtawki co tata). Można zauważyć, że jedna z dziewczynek znajduje się na końcu, ale druga trochę bliżej środka huśtawki. Zatem dziewczynki razem ważą więcej niż tata. Wskazuje to na prawdziwość stwierdzenia 3.
Nie można natomiast na podstawie podanych informacji, ani tekstowych ani graficznych, zdecydowanie ocenić, która z dziewczynek, Ania czy Basia, waży więcej. Z rysunku widać, że jedna z dziewczynek jest większa (a zatem cięższa) od drugiej, jednakże nie wiemy czy to jest Ania czy Basia. Nieprawdziwe jest zatem stwierdzenie 2.
Zadanie wykorzystano w badaniu przeprowadzonym w pierwszych klasach liceum ogólnokształcącego. Około 31% uczestników badania rozwiązało całe zadanie poprawnie. Najwięcej problemów sprawił punkt 3. Jedynie niecałe 39% badanych licealistów prawidłowo wywnioskowało, że suma ciężarów obu dziewczynek jest większa od ciężaru taty. Widać, że absolwenci gimnazjum nie rozumieją w pełni zasad działania prostych urządzeń mechanicznych, do których zalicza się dźwignia dwustronna. Pozostałe dwa stwierdzenia raczej nie sprawiły licealistom większych problemów. Prawidłowo zostały rozwiązane przez odpowiednio 93% i 80% uczestników badania.
Zadanie jest bardzo dobrym przykładem z życia, obrazującym zasadę działania dźwigni. Jednak wyniki uzyskane przez młodych ludzi pokazały, że dla wielu z nich ta zasada nie jest oczywista. Warto, aby nauczyciel po omówieniu tego zadania poświęcił jeszcze trochę czasu na dyskusję i przeanalizowanie z uczniami kilku innych przykładów dźwigni, takich jak waga szalkowa, nożyczki czy taczka. Nawet nasza ręka działa na zasadzie dźwigni. Chwytamy przedmiot w dłonie i podnosimy w górę dzięki umiejętności zginania ręki w łokciu.. Uczniowie sami mogą szukać w otoczeniu przykładów dźwigni (inne części ciała ludzkiego, elementy prostych urządzeń kuchennych jak otwieracze do konserw, słoików, itp.). Można pozwolić im budować dźwignię z linijki i gumki jako wspornika lub pozwolić na ich własne inwencje twórcze.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





