Wiązka zadań
Zależność prędkości od czasu
Zadanie
Dwa ciała poruszały się po tej samej trasie. Prędkość pierwszego ciała zmieniała się w czasie zgodnie z wykresem 1, a prędkość drugiego ciała – zgodnie z wykresem 2.
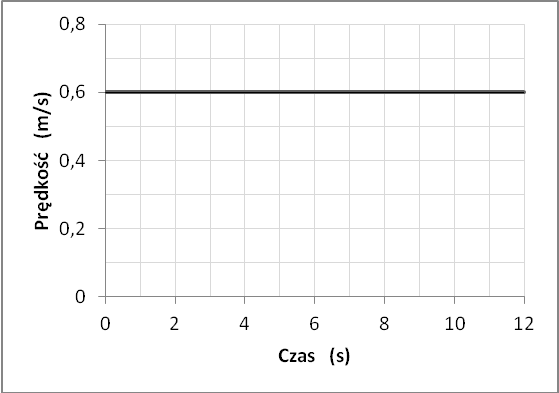
Wykres 1
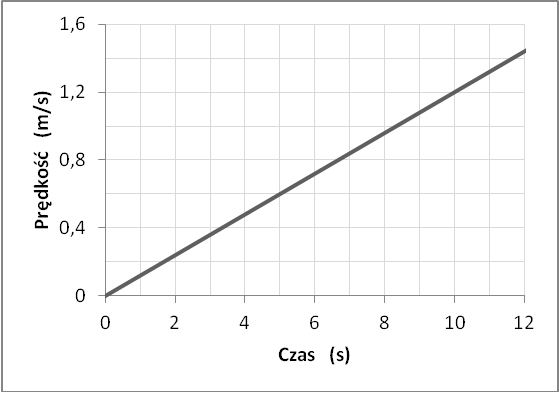
Wykres 2
Oceń prawdziwość poniższych stwierdzeń.
| Stwierdzenie | Czy jest prawdziwe? | |
| 1 | Oba ciała poruszały się ze stałą prędkością. | `square` TAK / `square` NIE |
| 2 | W chwili t = 5 s prędkości obu ciał były równe. | `square` TAK / `square` NIE |
| 3 | Oba ciała w czasie t = 10 s przebyły tę samą drogę. | `square` TAK / `square` NIE |
Poprawna odpowiedź
1.NIE., 2.TAK., 3TAK.
Wymaganie ogólne
1 Wykorzystanie wielkości fizycznych do opisu poznanych zjawisk lub rozwiązania prostych zadań obliczeniowych.
Wymaganie szczegółowe
1.1. Ruch prostoliniowy i siły. Uczeń posługuje się pojęciem prędkości do opisu ruchu/ przelicza jednostki prędkości
1.2. Ruch prostoliniowy i siły. Uczeń odczytuje prędkość i przebytą odległość z wykresów zależności drogi i prędkości od czasu, oraz rysuje te wykresy na podstawie opisu słownego
2.6. Energia. Uczeń analizuje jakościowo zmiany energii wewnętrznej spowodowane wykonaniem pracy i przepływem ciepła
8.8. Wymagania przekrojowe. Uczeń sporządza wykres na podstawie danych z tabeli (oznaczenie wielkości i skali na osiach) a także odczytuje dane z wykresu
Komentarz
Zadanie sprawdza umiejętność interpretacji wykresów na przykładzie zależności prędkości ciała od czasu trwania ruchu i zostało wykorzystane w badaniu, w którym wzięli udział uczniowie klas trzecich gimnazjum. Może ono pomóc w realizacji kilku punktów podstawy programowej, w szczególności kładących nacisk na przetwarzanie danych z postaci graficznej na słowną.
W przypadku pierwszego wykresu prędkość poruszającego ciała nie zmienia się w czasie (przyjmuje stałą wartość), zatem ciało to porusza się ruchem jednostajnym. Z drugiego wykresu możemy odczytać, że prędkość ciała rośnie liniowo wraz z czasem. W takim razie to ciało porusza się z pewnym przyspieszeniem. Zatem pierwsze ze stwierdzeń zestawionych w tabeli jest fałszywe. Takiej odpowiedzi udzieliło aż 89% uczniów biorących udział w badaniu.
Nieco więcej problemów uczniowie mieli z kolejną częścią zadania. Aby ją rozwiązać, należało znaleźć na osi czasu wartość t = 5 s, a następnie kolejno z obu wykresów odczytać, jaką prędkość osiągają opisane ciała we wskazanej chwili. Zarówno pierwsze, jak i drugie ciało poruszało się w chwili t = 5 s z prędkością równą 0,6 m/s, a zatem drugie stwierdzenie jest prawdziwe. Prawidłowej odpowiedzi udzieliło 75% uczestników badania.
Najbardziej problematyczna okazała się ocena trzeciego stwierdzenia. Aby na podstawie wykresu zależności prędkości od czasu wyznaczyć przebytą przez ciało drogę, można obliczyć pole pod wykresem. W przypadku pierwszego wykresu powinniśmy wyznaczyć pole prostokąta o bokach równych odpowiednio 10 s oraz 0,6 m/s. W przypadku drugiego wykresu należy znaleźć pole trójkąta o podstawie równej 10 cm i wysokości 1,2 m/s. Podstawienie tych wartości do odpowiednich wzorów prowadzi w obu przypadkach do tego samego wyniku (6 metrów), zatem ostatnie stwierdzenie jest prawdziwe. Inną metodą obliczenia drogi przebytej przez ciało jest wyznaczenia prędkości średniej i przemnożenie tej wielkości przez czas ruchu. W przypadku obu wykresów uzyskujemy dla pierwszych 10 sekund ruchu tę samą wartość prędkości średniej (0,6 m/s), zatem oba ciała przebyły w tym czasie tę samą drogę. Ta część zadania została prawidłowo rozwiązany przez 32% uczniów, przy czym różnicowała ona znacznie mocniej niż dwie poprzednie.
Prawidłowej oceny wszystkich trzech stwierdzeń dokonało tylko 17% osób biorących udział w badaniu. Oznacza to, że niemal połowa uczniów prawidłowo rozwiązujących ostatnią, najtrudniejszą część zadania, popełniała błędy na wcześniejszych etapach. Najprawdopodobniej uczniowie gimnazjum nie mają wystarczającej praktyki z wyznaczaniem niektórych wielkości fizycznych przy użyciu metod matematycznych i większość z nich nie wie, jak obliczyć przebytą drogę, posługując się wykresem zależności prędkości od czasu.
Być może dla części uczniów problem jest dużo szerszy – wyniki dotychczasowych badań przeprowadzonych przez Pracownię Przedmiotów Przyrodniczych sugerują, że na III etapie edukacyjnym uczniowie nienajlepiej radzą sobie z odczytywaniem i przetwarzaniem informacji przedstawionych w formie graficznej. Wskazane byłoby zatem systematyczne ćwiczenie tych umiejętności na różnych przykładach.
Uczniom szczególnie zainteresowanym przedmiotami ścisłymi (w szczególności matematyką i informatyką) można przy okazji omawiania tego zadania przybliżyć pojęcie całki oraz nawiązać do metod całkowania numerycznego. Najprawdopodobniej uczniowie ci spotkają się z tymi pojęciami na dalszych etapach edukacyjnych, niemniej warto oswoić ich już na poziomie gimnazjum z pewną terminologią i stworzyć podstawy do zdobywania bardziej zaawansowanych umiejętności z tej dziedziny.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





