Wiązka zadań
Alpy
Prezentowane zadania pochodzą z zestawu zadań badania Pracowni Przedmiotów Przyrodniczych „Laboratorium myślenia”. Wszelkie informacje dotyczące badania „Laboratorium myślenia” dostępne są na stronie eduentuzjasci.pl.
W masywie najwyższej góry Europy, Mont Blanc (4810 m n.p.m.), leży szczyt Aiguille du Midi (3842 m n.p.m.). Można wjechać na niego kolejką linową, której dolna stacja położona jest u podnóża góry, we francuskim mieście Chamonix.
Zadanie 1
Fotografia przedstawia napis nad wejściem do stacji kolejki w Chamonix.

Jaka jest względna i bezwzględna wysokość górnej stacji kolejki?
| Wysokość | Wartość | Jednostka | |
| 1. | bezwzględna |
`square` A. 968 / `square` B. 1030 `square` C. 2812 / `square` D. 3842 |
`square` I. m `square` II. m n.p.m. |
| 2. | względna |
`square` A. 968 / `square` B. 1030 `square` C. 2812 / `square` D. 3842 |
`square` I. m `square` II. m n.p.m. |
Poprawna odpowiedź
1 – D, II
2 – C, I
Wymaganie ogólne
2.1 Identyfikowanie związków i zależności oraz wyjaśnianie zjawisk i procesów. Uczeń posługuje się podstawowym słownictwem geograficznym w toku opisywania oraz wyjaśniania zjawisk i procesów zachodzących w środowisku geograficznym.
2.2 Identyfikowanie związków i zależności oraz wyjaśnianie zjawisk i procesów. Uczeń identyfikuje związki i zależności w środowisku przyrodniczym, gospodarce i życiu społecznym w różnych skalach przestrzennych (lokalnej, regionalnej, krajowej, globalnej)
Wymaganie szczegółowe
9.8. Europa. Relacje przyroda – człowiek – gospodarka. Uczeń wykazuje wpływ gór na cechy środowiska przyrodniczego oraz gospodarkę krajów alpejskich.
Komentarz
Zadanie sprawdza zrozumienie pojęć: „wysokość względna” i „wysokość bezwzględna” oraz umiejętność przeprowadzania prostych obliczeń związanych z tymi wysokościami. Aby udzielić pełnej odpowiedzi, uczeń musi również wiedzieć, w jakich jednostkach wyraża się wysokość względną, a w jakich – bezwzględną.
Zadanie wykorzystuje fotografię przedstawiającą tablicę umieszczoną przy dolnej stacji kolejki górskiej we francuskim mieście Chamonix.
Uczeń rozwiązujący zadanie powinien zapoznać się z informacjami zawartymi na tablicy, na której obok obcojęzycznych nazw podane są dwie liczby. Kluczem do prawidłowego rozwiązania jest zrozumienie sensu podania na tablicy informacyjnej właśnie tych dwu liczb – wysokości dolnej i górnej stacji kolejki. Uczeń powinien rozumieć, że opis umieszczony nad wejściem dotyczy wysokości liczonych od poziomu morza, co dla ułatwienia podano w opisie poprzedzającym zadanie. Nie wiadomo, dlaczego na tablicy zastosowano tylko jeden rodzaj jednostek wysokości, ale dzięki temu można było skonstruować tego rodzaju zadanie, to znaczy zapytać uczniów nie tylko o wartości liczbowe, ale i o jednostki, w jakich wyraża się obie wysokości.
Do rozwiązania pierwszej części zadania należy spośród liczb wymienionych na tablicy wybrać wysokość górnej stacji kolejki.
Na podstawie niżej zamieszczonego wykresu można przeanalizować, jak uczniowie rozwiązywali tę część zadania. Około 20% najsłabszych uczniów udzieliło poprawnej odpowiedzi, natomiast wśród uczniów najlepszych odsetek ten wzrasta do około 85%. Ogółem 43% badanych uczniów poprawnie rozwiązało tę część zadania.
Charakterystycznym błędem, który prezentuje żółta linia odpowiedzi B, jest wybieranie, zwłaszcza przez uczniów słabszych, wysokości dolnej stacji kolejki. Być może uczniowie, którzy wybrali tę odpowiedź, nieuważnie przeczytali polecenie i odczytali wysokość stacji dolnej zamiast górnej.
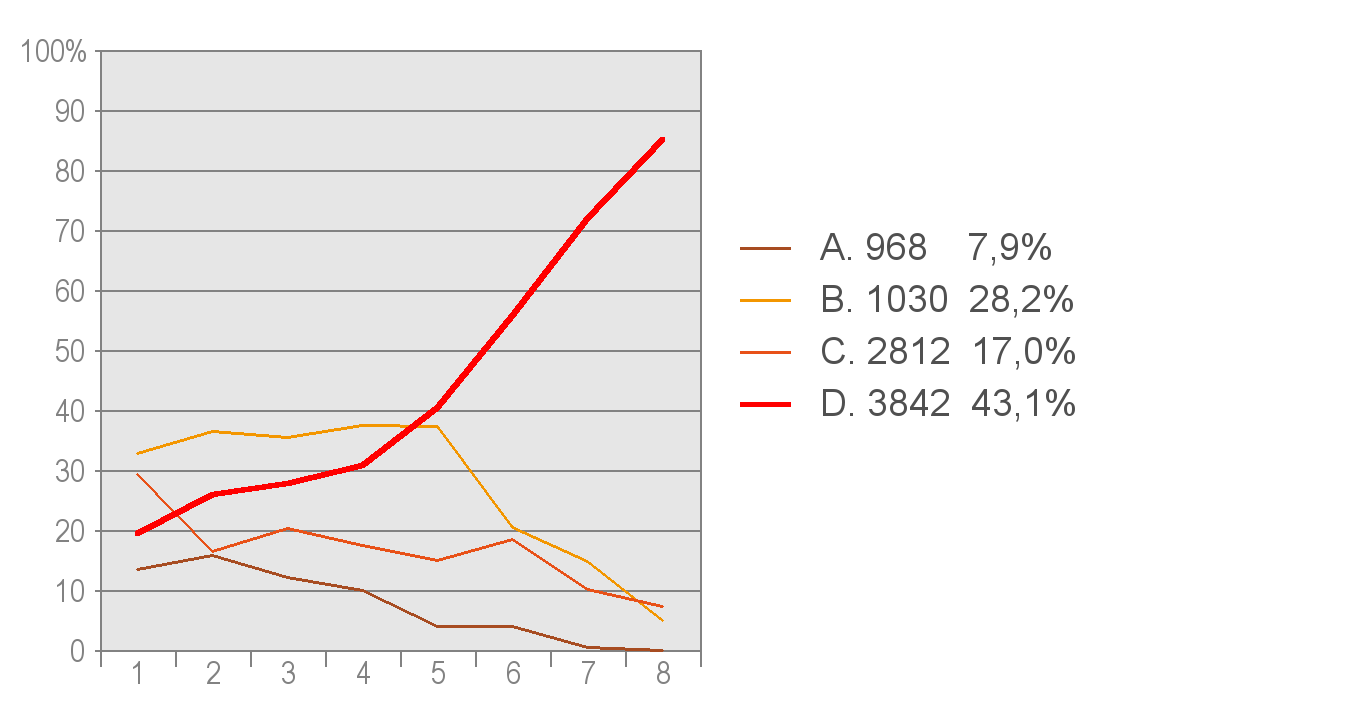 Wykres 1. Rozkład częstości odpowiedzi na pytanie o wysokość bezwzględną górnej stacji kolejki. Na osi X zaznaczono poziom ucznia (1 – grupa uczniów, którzy uzyskali najniższe wyniki w całym teście, 8 – grupa o najwyższych wynikach), na osi Y zaś – odsetek uczniów z danej grupy, którzy wybrali daną odpowiedź. Wartości nie sumują się do 100%, ponieważ pewna część uczniów nie wybrała żadnej odpowiedzi.
Wykres 1. Rozkład częstości odpowiedzi na pytanie o wysokość bezwzględną górnej stacji kolejki. Na osi X zaznaczono poziom ucznia (1 – grupa uczniów, którzy uzyskali najniższe wyniki w całym teście, 8 – grupa o najwyższych wynikach), na osi Y zaś – odsetek uczniów z danej grupy, którzy wybrali daną odpowiedź. Wartości nie sumują się do 100%, ponieważ pewna część uczniów nie wybrała żadnej odpowiedzi.
Drugim etapem rozwiązania zadania jest obliczenie wysokości względnej górnej stacji kolejki. W tym celu uczeń powinien wykonać proste działanie – odjąć wysokość dolnej stacji od wysokości stacji górnej. Poprawną odpowiedź wskazało 31% badanych, ale nieznacznie więcej (33,6%) uczniów wskazało wartość wysokości bezwzględnej szczytu.
Wyniki tej części zadania możemy prześledzić na poniższym wykresie.
Słabsi uczniowie nie dostrzegli konieczności wykonania obliczeń i wskazywali jedną z dwu wartości bezwzględnych, odczytanych z tablicy. Obie odpowiedzi (B i D) były oczywiście błędne. Jedynie najlepsi uczniowie dokonali obliczeń i potrafili udzielić poprawnej odpowiedzi.
 Wykres 2. Rozkład częstości odpowiedzi na pytanie o wysokość względną górnej stacji kolejki. Oznaczenia takie same, jak na wykresie 1.
Wykres 2. Rozkład częstości odpowiedzi na pytanie o wysokość względną górnej stacji kolejki. Oznaczenia takie same, jak na wykresie 1.
Uczeń, który rozumie, co oznaczają określenia wysokość względna i bezwzględna, powinien przyporządkować im właściwe jednostki. Prawie 60% badanych uczniów poprawnie przyporządkowało jednostki w pierwszym wierszu zadania, a niemal 57% – w drugim.
Za poprawne rozwiązanie całego zadania uważa się dokonanie czterech prawidłowych wyborów. Dokonało tego jedynie 18,7% uczniów. Ostatni wykres ilustruje, jak rozwiązywali całe zadanie uczniowie z poszczególnych grup. Można na nim zauważyć, że zadanie jako całość było na tyle trudne, iż przewaga odpowiedzi poprawnych nad błędnymi pojawia się tylko w grupie najzdolniejszych uczniów. Zadanie bardzo dobrze różnicuje uczniów, co można wywnioskować po stromym nachyleniu linii poprawnych odpowiedzi. Im słabsi uczniowie, tym mniej poprawnych rozwiązań całego zadania.
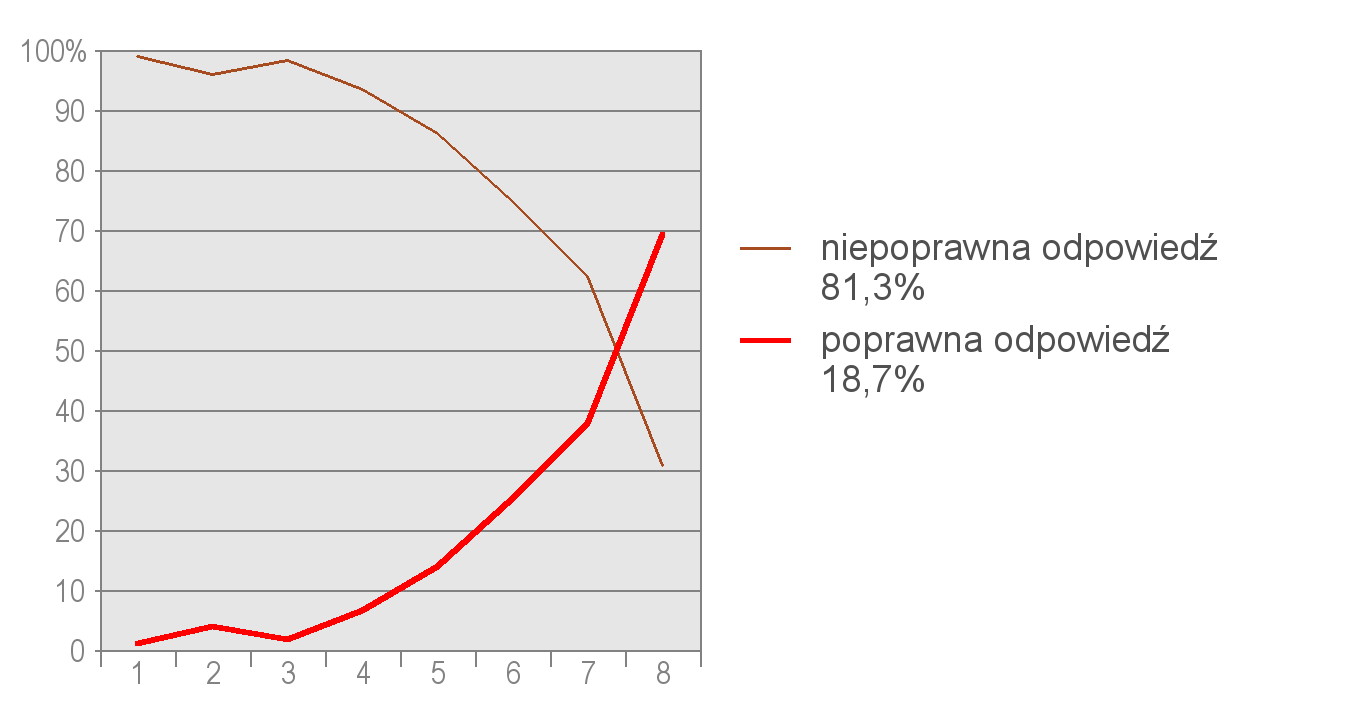 Wykres 3. Rozkład częstości odpowiedzi poprawnych i niepoprawnych w całym zadaniu. Oznaczenia takie same, jak na wykresie 1.
Wykres 3. Rozkład częstości odpowiedzi poprawnych i niepoprawnych w całym zadaniu. Oznaczenia takie same, jak na wykresie 1.
Forma przedstawienia wysokości dolnej i górnej stacji kolejki górskiej odbiega od starannie dobranych danych przedstawianych w podręcznikach. Dzięki temu zadanie sprawdzało, czy badani uczniowie potrafiliby posługiwać się wiedzą w sytuacji praktycznej. W życiu codziennym nie da się uniknąć sytuacji, gdy trzeba rozumieć zastane informacje. W górach Europy i świata raczej nie spotkamy „szkolnego” sposobu przedstawienia wysokości bezwzględnej. W Alpach, o których pośrednio mówi to zadanie, nie używa się określenia wysokości z podaniem skrótu „n.p.m.”
Być może zadanie byłoby łatwiejsze, gdyby zamiast podania słownictwa geograficznego polecono uczniom obliczenie różnicy wysokości pokonywanej przez kolejkę. Byłoby to również zadanie praktyczne, ale nie sprawdziłoby w pełny sposób rozumienia użytych pojęć geograficznych.
Zadanie 2
(1) Po wyjechaniu na szczyt można się spodziewać temperatury
`square` A. wyższej, / `square` B. niższej,
(2) ponieważ wraz ze wzrostem wysokości bezwzględnej temperatura
`square` A. spada. / `square` B. wzrasta.
(3) Na szczycie należy oczekiwać ciśnienia
`square` A. wyższego, / `square` B. niższego,
(4) ponieważ wraz ze wzrostem wysokości bezwzględnej ciśnienie
`square` A. spada. / `square` B. wzrasta.
Poprawna odpowiedź
1.B,
2.A,
3.B,
4.A
Wymaganie ogólne
2.1 Identyfikowanie związków i zależności oraz wyjaśnianie zjawisk i procesów. Uczeń posługuje się podstawowym słownictwem geograficznym w toku opisywania oraz wyjaśniania zjawisk i procesów zachodzących w środowisku geograficznym.
2.2 Identyfikowanie związków i zależności oraz wyjaśnianie zjawisk i procesów. Uczeń identyfikuje związki i zależności w środowisku przyrodniczym, gospodarce i życiu społecznym w różnych skalach przestrzennych (lokalnej, regionalnej, krajowej, globalnej)
2.3 Identyfikowanie związków i zależności oraz wyjaśnianie zjawisk i procesów. Uczeń rozumie wzajemne relacje przyroda-człowiek.
Wymaganie szczegółowe
3.1. Wybrane zagadnienia geografii fizycznej. Uczeń charakteryzuje wpływ głównych czynników klimatotwórczych na klimat.
Komentarz
Zaprezentowane zadanie wydaje się dość proste. Oczekujemy, że uczeń wskaże prawidłowości zmian składników pogody, gdy wzrasta wysokość nad poziomem morza. Wydaje się, że określenie spadku temperatury i ciśnienia atmosferycznego nie powinno sprawić problemów, choćby dlatego, że polscy alpiniści i himalaiści tworzą historię zdobywania najwyższych szczytów świata i dość często w mediach możemy śledzić ich zmagania. Zazwyczaj wtedy można się dowiedzieć, że w górach jest dużo chłodniej, ponieważ ze wzrostem wysokości obniża się temperatura oraz że trudno jest ugotować sobie posiłek, gdyż im wyżej, tym jest niższe ciśnienie atmosferyczne i woda ma niższą temperaturę wrzenia.
Wydaje się, że łatwiej opanować i zapamiętać zmiany temperatury związane ze zmianą wysokości, gdyż z informacji w mediach o akcjach górskich większości osób z pewnością utkwi w pamięci widok zaśnieżonych szczytów. Znajomość tej zależności utrwala się dodatkowo zadaniami, w których uczeń oblicza, jakiej temperatury można się spodziewać na pewnej wysokości.
Trudniej zapamiętać prawidłowości zmian ciśnienia atmosferycznego. Dlatego szczególny nacisk przy omawianiu zagadnień związanych z klimatem górskim, oraz z ciśnieniem atmosferycznym (zarówno na geografii, jak i fizyce), należy położyć na omówienie zmian ciśnienia atmosferycznego w zależności od wysokości. Wyniki tego zadania potwierdzają przypuszczenie o różnym stopniu trudności tych zagadnień.
Poniżej zaprezentowano wykresy, na których można prześledzić, jakich odpowiedzi udzielali uczniowie w kolejnych wierszach zadania. Wszystkich uczniów biorących udział w badaniu podzielono w zależności od uzyskanego wyniku na osiem grup o równej liczebności. Te grupy uczniów zaznaczono na osi poziomej wykresu (grupa 1 – uczniowie o najniższych wynikach, grupa 8 – uczniowie o wynikach najwyższych).
Z osi pionowej odczytamy natomiast odsetek uczniów w danej grupie, którzy udzielili określonej odpowiedzi.
Z wykresu możemy odczytać, że im lepszy wynik ogólny ucznia, tym więcej poprawnych odpowiedzi w wierszach 1. i 2. dotyczących zmiany temperatury powietrza. Wartości nie sumują się do 100%, ponieważ pewna część uczniów nie wybrała żadnej odpowiedzi.
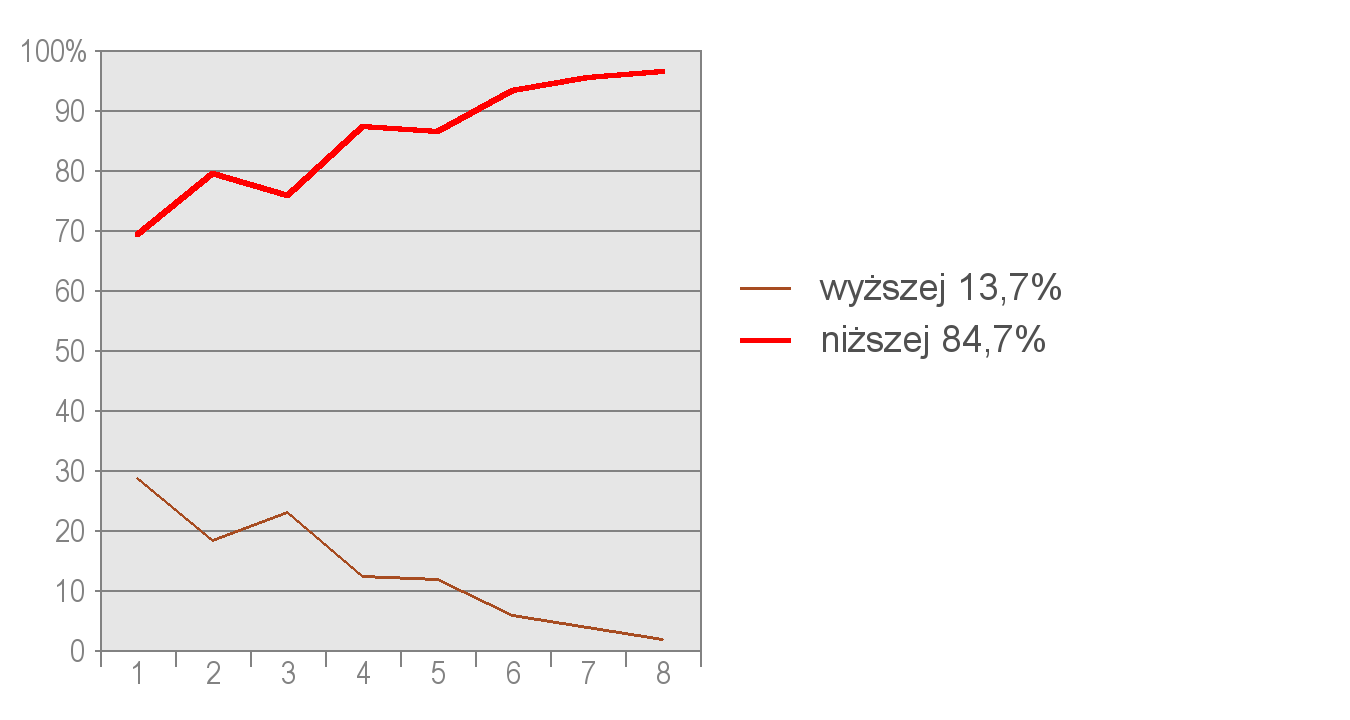
Wykres 1. Rozkład częstości odpowiedzi na pytanie o zmianę temperatury po wjechaniu na szczyt. Na osi X zaznaczono poziom ucznia (1 – grupa uczniów, którzy uzyskali najniższe wyniki w całym teście, 8 – grupa o najwyższych wynikach), na osi Y zaś – odsetek uczniów z danej grupy, którzy wybrali daną odpowiedź. Wartości nie sumują się do 100%, ponieważ pewna część uczniów nie wybrała żadnej odpowiedzi.
Wykres 2. Rozkład częstości odpowiedzi na pytanie o związek między zmianą wysokości n.p.m. a zmianą temperatury. Oznaczenia takie same, jak na wykresie 1.
W kolejnych dwu wierszach sprawdzamy znajomość zmian ciśnienia atmosferycznego zachodzących wraz ze wzrostem wysokości:
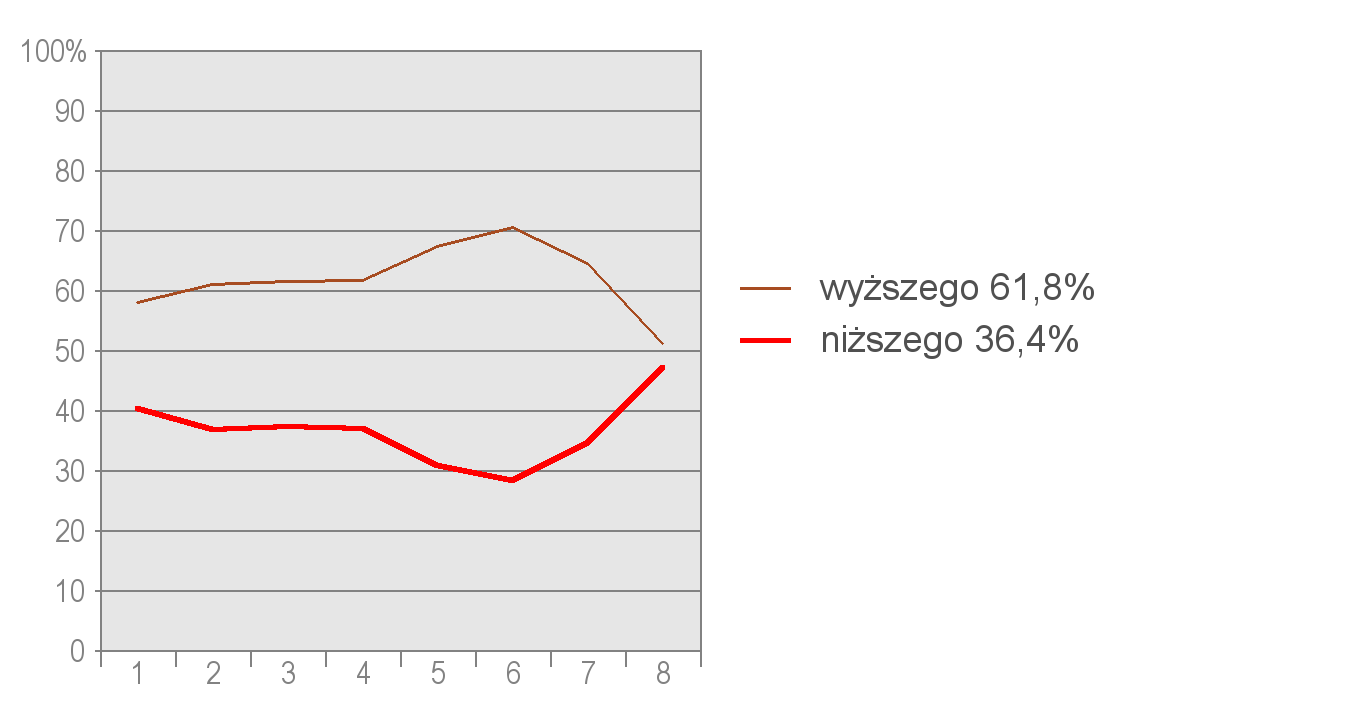
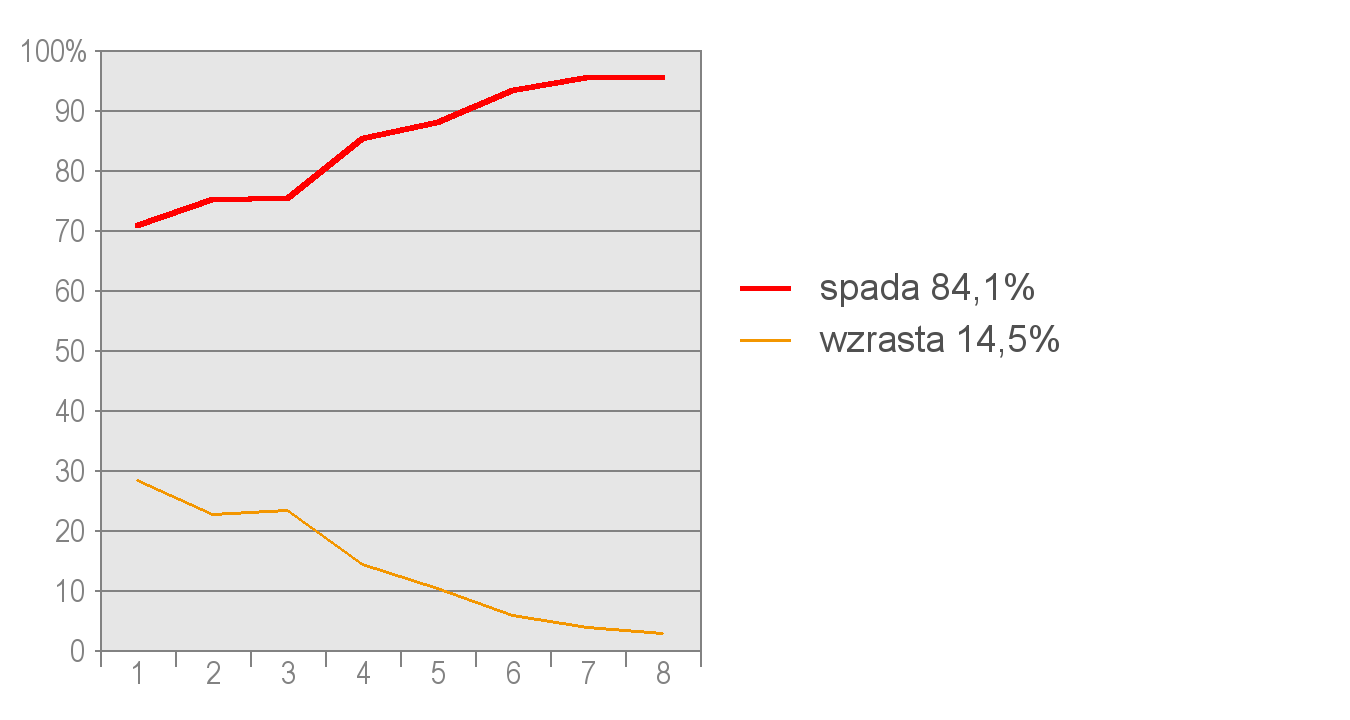
Wykres 3. Rozkład częstości odpowiedzi na pytanie o zmianę ciśnienia po wjechaniu na szczyt. Oznaczenia takie same, jak na wykresie 1.
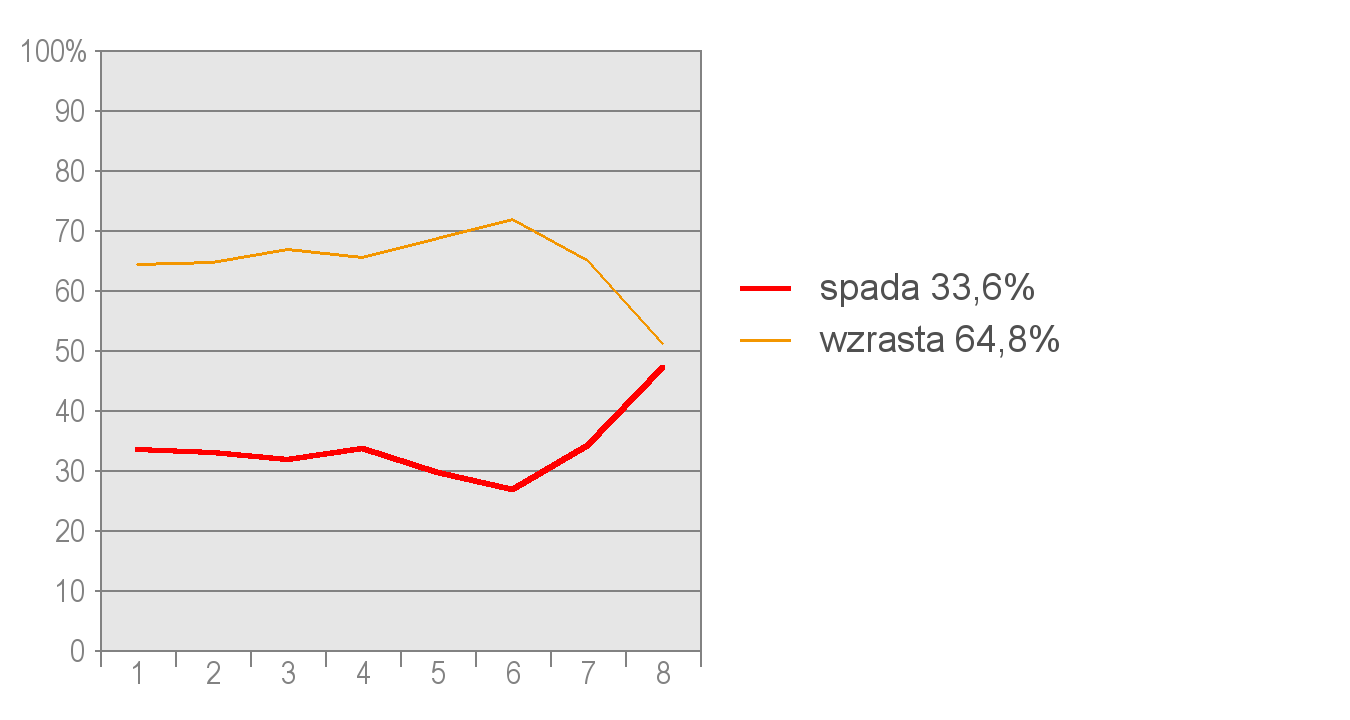
Wykres 4. Rozkład częstości odpowiedzi na pytanie o związek między zmianą wysokości n.p.m. a zmianą ciśnienia. Oznaczenia takie same, jak na wykresie 1.
Z powyższych wykresów wynika, że uczniowie lepiej opanowali zależność spadku temperatury niż spadku ciśnienia wraz ze wzrostem wysokości. W wierszu 1. uczniowie udzielili 84,7% prawidłowych odpowiedzi, w wierszu 2. – 84,1%.
Z wykresów dotyczących wierszy 1. i 2. można również wywnioskować, że sposób sformułowania polecenia był jasny i nie wprowadził w błąd uczniów osiągających lepsze wyniki, którzy mogli wiedzieć także o zjawisku inwersji temperatur. Polega ono na odwróceniu temperatur: wychłodzone, zimne powietrze zalega w dolinach i kotlinach, a cieplejsze, lżejsze, jest wypierane ku górze. Jednak sformułowanie polecenia jest wystarczająco jednoznaczne, na co wskazuje systematyczny, równomierny wzrost liczby poprawnych odpowiedzi w coraz wyższych grupach uczniów.
Okazało się, że uczniowie mieli problemy z ustaleniem zależności ciśnienia atmosferycznego od wysokości. W wierszu 3. tylko 36,4% uczniów odpowiedziało poprawnie, a w wierszu 4. – tylko 33,6%. Logiczne jest, że przy wyborze niższego ciśnienia (odpowiedź A. w wierszu 3.) powinien być wybrany jego spadek (odpowiedź A. w wierszu 4.). Prawdopodobnie uczniowie nie zawsze wiedzieli o zależności ciśnienia atmosferycznego od wysokości, ale przeczytali zadanie ze zrozumieniem i próbowali je poprawnie rozwiązać. Uczniowie, którzy nie rozumieli zależności między ciśnieniem a wysokością i w dwu końcowych wierszach popełnili błąd, zapewne wybrali odpowiedzi „na krzyż”, wnioskując że skoro raz był spadek, to teraz kolej na wzrost wymienionych w zadaniu wartości. Jest to jeden ze sposobów radzenia sobie z zadaniami, a może raczej – nawyk rozwiązywania zadań testowych, na które uczeń nie zna prawidłowej odpowiedzi. Na wykresach możemy zaobserwować, że dopiero w ostatnich grupach uczniów o najwyższych wynikach, liczba poprawnych odpowiedzi dotyczących ciśnienia wzrasta.
Zastanawia również fakt, że uczniowie „średni”, czyli ci, którzy znaleźli się w grupach 4, 5 i 6, w tej części zadania odpowiedzieli gorzej niż uczniowie z najniższych grup. Możliwe, że przyczyną było szukanie przez tych uczniów ukrytej ich zdaniem w zadaniu trudności.
Reasumując: zadanie uznawano za prawidłowo rozwiązane, gdy uczeń udzielił poprawnych odpowiedzi we wszystkich czterech wierszach. Tylko 23,8% osób rozwiązało je poprawnie. Zadanie różnicowało tylko najlepszych uczniów. Pierwsza jego część była zdecydowanie łatwiejsza, zaś druga zaważyła o niskim wyniku dla całego zadania. Wyniki dla całego zadania przedstawia kolejny wykres:
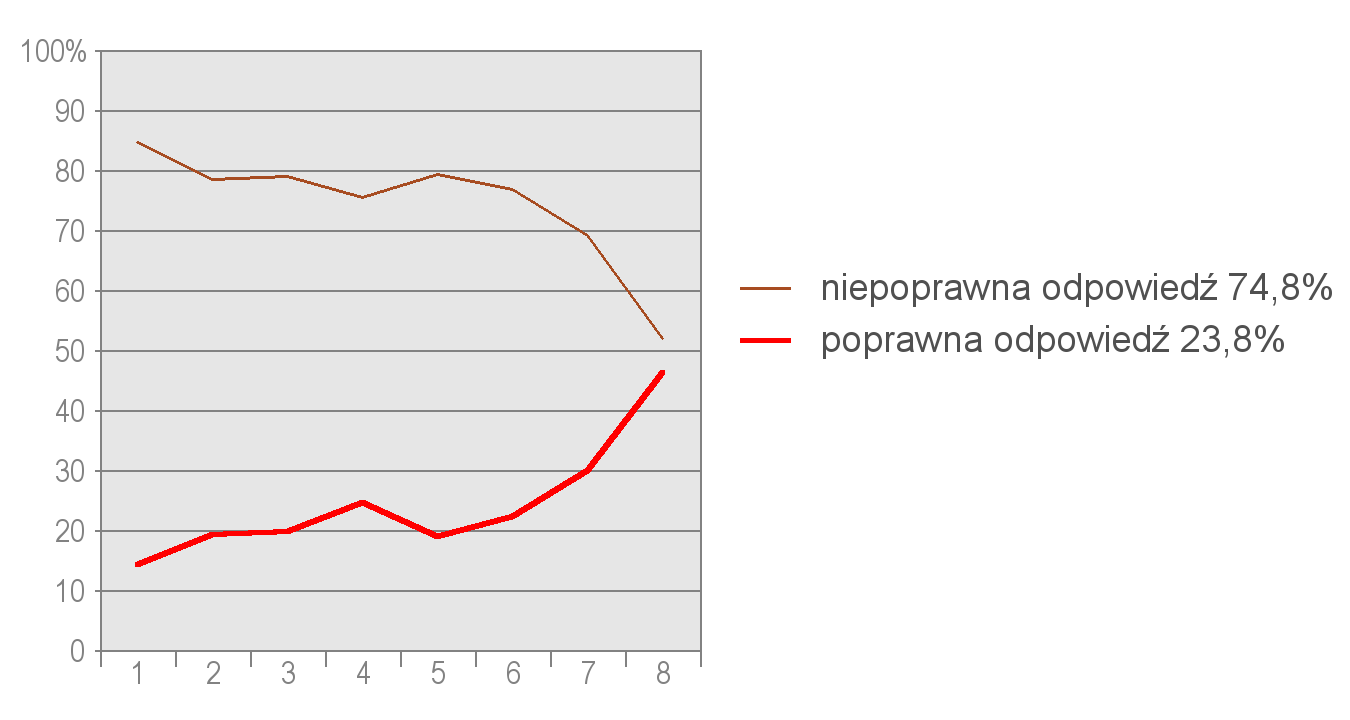
Wykres 5. Rozkład częstości odpowiedzi poprawnych i niepoprawnych w całym zadaniu. Oznaczenia takie same, jak na wykresie 1.
Wydaje się, że powracanie do zagadnienia może pomóc uczniom w zapamiętaniu omówionych zależności. Zagadnienia poświęcone ciśnieniu można omawiać w czasie lekcji o klimacie. Później można je utrwalać zawsze wtedy, gdy omawiane są górskie krajobrazy, na przykład krajów alpejskich. Utrwalanie zagadnień i współpraca międzyprzedmiotowa z nauczycielami fizyki powinny pomóc w opanowaniu tych trudnych, jak się okazało, zagadnień.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





