Wiązka zadań
Piec do wytwarzania nanodrutów
Piec w którym otrzymuje się nanodruty (czyli druciki o średnicy mniejszej od 0,1 mikrometra), wykorzystywane do budowy niektórych nowoczesnych urządzeń elektronicznych, jest wyposażony w specjalną rurę grzejną (rysunek 1). Temperatura w piecu, mierzona przy jego podłożu, jest najwyższa w środku, a najniższa przy obu jego końcach (rysunek 2).

Rys. 1. Schemat budowy pieca

Rys. 2. Wykres zależności temperatury w piecu, mierzonej przy podłożu, od odległości od jego lewego końca.
Prezentowana wiązka zadań została wykorzystano w badaniu, w którym wzięli udział uczniowie klas trzecich gimnazjum. Tematyka zadań jest nietypowa jak na ten etap edukacyjny i dotyczy metodologii wytwarzania nanodrutów. Wprawdzie zagadnienie to jest przedmiotem zainteresowania wielu laboratoriów naukowych, a same nanodruty znajdują coraz szersze zastosowanie, niemniej poniższa wiązka niekoniecznie musi służyć do rozbudzania ciekawości naukowej uczniów. Poszczególne zadania mierzą konkretne umiejętności złożone, związane z odczytywaniem i przetwarzaniem informacji przedstawionych w formie wykresów i schematów. Dzięki nawiązaniu do zupełnie nowej, z perspektywy ucznia, tematyki, do rozwiązania tych zadań nie jest konieczna wiedza pamięciowa – w zupełności wystarczą informacje zawarte w tekście. Warto wykorzystać poniższe zadania na lekcji, czy to w celu sprawdzenia, na ile uczniowie radzą sobie z wykresami, czy też w celu treningu odpowiednich umiejętności.
Zadanie 1
Na podstawie zamieszczonych rysunków oceń prawdziwość poniższych stwierdzeń.
| Stwierdzenie | Czy jest prawdziwe? | |
| 1. |
Temperatura w piecu rośnie proporcjonalnie z odległością od jego lewego końca. |
`square` Tak / `square` Nie |
| 2. | Temperatura próbki umieszczonej w sektorze S2 nie przekracza 400°C. | `square` Tak / `square` Nie |
| 3. | Maksymalna temperatura jaką można uzyskać przy podłożu tego pieca wynosi 1500°C. | `square` Tak / `square` Nie |
Poprawna odpowiedź
1 - Nie,
2 - Tak,
3 - Nie
Wymaganie ogólne
4 Posługiwanie się informacjami pochodzącymi z analizy przeczytanych tekstów (w tym popularno-naukowych).
Wymaganie szczegółowe
8.7. Wymagania przekrojowe. Uczeń rozpoznaje proporcjonalność prostą na podstawie danych liczbowych lub na podstawie wykresu oraz posługuje się proporcjonalnością prostą
8.8. Wymagania przekrojowe. Uczeń sporządza wykres na podstawie danych z tabeli (oznaczenie wielkości i skali na osiach) a także odczytuje dane z wykresu
8.9. Wymagania przekrojowe. Uczeń rozpoznaje zależność rosnącą i malejącą na podstawie danych z tabeli lub na podstawie wykresu oraz wskazuje wielkość maksymalną i minimalną
Komentarz
W przypadku tego zadania uczeń na podstawie tekstu i zamieszczonych wykresów powinien dokonać oceny prawdziwości stwierdzeń zestawionych w tabeli. Na rysunku 1 został przedstawiony schemat budowy pieca do wytwarzania nanodrutów. W piecu tym można wyróżnić dziesięć sektorów każdy o długości 10 cm. Na rysunku zaznaczono tylko pięć pierwszych sektorów, znajdujących się w lewej połowie pieca, ponieważ tylko do tych sektorów odnosi się rysunek 2, ilustrujący zależność temperatury panującej w danym sektorze od jego odległości od lewego końca pieca.
Pierwsze stwierdzenie prawidłowo oceniło jedynie 37% osób biorących udział w badaniu, zauważając, że wzrost temperatury w piecu nie jest proporcjonalny do odległości od jego lewego końca. Wiersz ten byłby prawdziwy, gdyby na rysunku 2 zależność była przedstawiona za pomocą linii prostej. Tymczasem z wykresu wynika, że zależność ta jest opisana znacznie bardziej skomplikowaną funkcją. Prawdopodobnie uczniowie udzielający nieprawidłowej odpowiedzi nie rozumieli, co oznacza stwierdzenie „rośnie proporcjonalnie z” i sam wzrost temperatury uznali za kryterium przesądzające o prawdziwości ocenianego stwierdzenia.
Znacznie mniej problematyczne okazało się stwierdzenie drugie. W tym przypadku aż 82% uczniów odpowiedziało prawidłowo, że temperatura próbki umieszczonej w sektorze S2 nie przekracza 400°C. Aby rozwiązać tę część zadania należało sprawdzić w jakim zakresie odległości od lewego końca pieca znajduje się sektor S2. Z rysunku 1 odczytujemy, że sektor ten mieści się pomiędzy 10. a 20. centymetrem pieca. Posługując się rysunkiem 2 ustalamy z kolei, że panują w nim temperatury nie przekraczające 400°C.
Najmniej kłopotów sprawiło uczniom stwierdzenie trzecie. Jego rozwiązywalność wyniosła w badaniu 93%. Z wykresu 2 odczytujemy, że temperatura w środku pieca nie przekracza 1400° C, co przesądza o nieprawdziwości stwierdzenia „maksymalna temperatura jaką można uzyskać w piecu wynosi 1500°C”. Całość zadania rozwiązało 31% uczniów, przy czym warto zauważyć, że większość osób prawidłowo oceniających pierwsze stwierdzenie, oceniła prawidłowo również dwa pozostałe. Zadanie to sprawdza umiejętność przetwarzania informacji przedstawionych w formie graficznej. Można wykorzystać je na lekcji, w celu przećwiczenia z uczniami umiejętności pracy z wykresem. Może ono również okazać się przydatne do zapoznania uczniów z konkretnymi zastosowaniami matematyki w fizyce. W tym przypadku rysunek 2 może posłużyć do wprowadzenia pojęcia zależności nieliniowej oraz wartości maksymalnej i minimalnej.
Zadanie 2
Załóżmy, że chcemy wykorzystać piec do wytwarzania nanodrutów w innym celu. W których dwóch sektorach pieca należy umieścić tlenek cyny(IV), aby na pewno uległ on stopieniu, ale aby jednocześnie nie doprowadzić go do wrzenia? Temperatura topnienia cyny w warunkach panujących w piecu wynosi 950° C, a temperatura jej wrzenia to 1600° C.
| Sektor | Wstaw X, jeżeli można w tym sektorze umieścić próbkę |
| S1 | |
| S2 | |
| S3 | |
| S4 | |
| S5 |
Poprawna odpowiedź
S4,
S5
Wymaganie ogólne
1 Wykorzystanie wielkości fizycznych do opisu poznanych zjawisk lub rozwiązania prostych zadań obliczeniowych.
4 Posługiwanie się informacjami pochodzącymi z analizy przeczytanych tekstów (w tym popularno-naukowych).
Wymaganie szczegółowe
2.9. Energia. Uczeń opisuje zjawiska topnienia, krzepnięcia, parowania, skraplania, sublimacji i resublimacji
8.2. Wymagania przekrojowe. Uczeń wyodrębnia zjawisko z kontekstu, wskazuje czynniki istotne i nieistotne dla wyniku doświadczenia
8.8. Wymagania przekrojowe. Uczeń sporządza wykres na podstawie danych z tabeli (oznaczenie wielkości i skali na osiach) a także odczytuje dane z wykresu
Komentarz
Zadanie to sprawdza umiejętność wnioskowania na podstawie tekstu, jak również umiejętność rozumienia informacji przedstawionej w postaci graficznej (w tym przypadku – wykresu). Zadanie stawia ucznia przed problemem do rozwiązania: należy wskazać te sektory pieca, w których tlenek cyny (IV) ulegnie stopnieniu, ale nie zostanie doprowadzony do wrzenia. Z tekstu dowiadujemy się, że w warunkach panujących w piecu cyna topi się w temperaturze 950o C, a wrze – w temperaturze 1600° C.
Na podstawie rysunku 1 ustalamy, że długość każdego sektora wynosi 10 cm. Zgodnie z rysunkiem 2 w żadnym miejscu pieca temperatura nie przekracza 1400° C, zatem z pewnością cyna nie zostanie doprowadzona do wrzenia, niezależnie od tego w którym sektorze ją umieścimy. Teraz musimy sprawdzić, w których sektorach temperatura jest wystarczająca, aby stopić cynę. Odpowiednie warunki zostają osiągnięte dopiero w odległości wynoszącej niespełna 30 cm od lewego końca pieca – w sektorach S1 i S2 nie osiągamy wystarczająco wysokiej temperatury. Zauważmy, że miejsce w którym panuje temperatura wystarczająca do stopienia cyny znajduje się na prawym końcu sektora S3. Temperatura na lewym końcu tego samego sektora jest jednak znacznie niższa – wynosi 400° C. Umieszczenie cyny w tym sektorze nie gwarantuje zatem jej roztopienia. Tylko w sektorach S4 i S5 cyna na pewno ulegnie stopieniu. Takiej odpowiedzi udzieliło 25% osób biorących udział w badaniu.
Jakkolwiek gimnazjaliści nie mieli większych wątpliwości co do sektorów S1 i S2 (w obu przypadkach wskazało je błędnie jako miejsca spełniające założone warunki zaledwie kilkanaście procent uczniów) to sektor S3 błędnie wskazało już 37% osób. Także w przypadku sektorów S4 i S5 osoby biorące udział w badaniu miały sporo wątpliwości – rozwiązywalność tych wierszy wynosiła odpowiednio 59 i 47%.
Zadanie 3
Który z poniższych wykresów przedstawia zależność temperatury od odległości od lewego końca pieca? Zwróć uwagę, że zakres odległości na poniższych wykresach to 50 do 100 cm od lewego końca pieca. Zakreśl prawidłową odpowiedź.
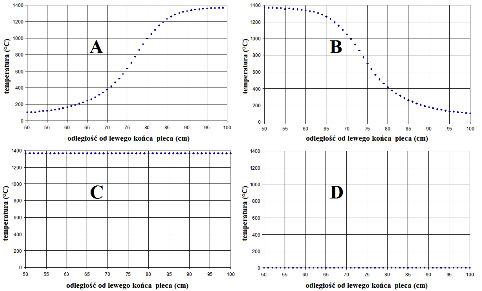
Rysunek własny, autor: Michał Sitarz
`square` A.
`square` B.
`square` C.
`square` D.
Poprawna odpowiedź
B
Wymaganie ogólne
1 Wykorzystanie wielkości fizycznych do opisu poznanych zjawisk lub rozwiązania prostych zadań obliczeniowych.
4 Posługiwanie się informacjami pochodzącymi z analizy przeczytanych tekstów (w tym popularno-naukowych).
Wymaganie szczegółowe
8.8. Wymagania przekrojowe. Uczeń sporządza wykres na podstawie danych z tabeli (oznaczenie wielkości i skali na osiach) a także odczytuje dane z wykresu
8.9. Wymagania przekrojowe. Uczeń rozpoznaje zależność rosnącą i malejącą na podstawie danych z tabeli lub na podstawie wykresu oraz wskazuje wielkość maksymalną i minimalną
Komentarz
We wstępie do zadania zamieszczony został wykres zależności temperatury w piecu od odległości od jego lewego końca w zakresie odległości od 0 do 50 cm. Aby rozwiązać zadanie uczeń powinien wskazać analogiczny wykres, sporządzony dla zakresu odległości od 50 do 100 cm. Należy przy tym pamiętać, że temperatura jest najwyższa w środku pieca, a najniższa na jego końcach. Skoro piec ma długość 100 cm, oznacza to, że maksymalna wartość temperatury jest osiągana w odległości 50 cm od jego lewego końca, a wartości minimalne – w odległościach 0 i 100 cm. Jeśli ograniczymy się do zakresu odległości podanego w zadaniu, okazuje się, że warunki te spełnia jedynie wykres przedstawiony na rysunku B. Jako prawidłową odpowiedź wskazało ten wykres 50% osób biorących udział w badaniu.
Najczęściej wybieraną odpowiedzią nieprawidłową była odpowiedź A (25% zaznaczeń). Być może część uczniów nie doczytała uważnie treści zadania i nie zrozumiała, że na podstawie podanych informacji mają znaleźć wykres będący „kontynuacją” wykresu przedstawionego we wstępie. Rzadziej wskazywany był wykres C – 15% uczniów wybrało taką odpowiedź. W tym przypadku uczniowie prawdopodobnie nie zrozumieli informacji dotyczącej wartości temperatury osiąganych na końcach pieca, dlatego też wskazali wykres, który wprawdzie da się połączyć z wykresem przedstawionym we wstępie w punkcie odległym o 50 cm od lewego końca pieca, jednak dalszy przebieg funkcji ilustrującej zależność temperatury od odległości nie odzwierciedla już warunków opisanych w zadaniu. Na odpowiedź D zdecydowało się najmniej, bo zaledwie 7% osób. Najprawdopodobniej byli to uczniowie, którzy wybierali odpowiedź losowo.
Uzyskane wyniki sugerują, że uczniowie gimnazjum mają spore trudności z interpretacją wykresów oraz powiązaniem informacji tekstowej z informacją graficzną. Na ten sam problem wskazują wyniki uzyskane dla innych zadań wymagających pracy z wykresami lub schematami, dlatego warto na lekcji poświęcić nieco czasu na kształtowanie tego typu umiejętności. Dobrą okazją do treningu umiejętności sporządzania i odczytywania wykresów mogą być wszelkiego rodzaju ćwiczenia doświadczalne, w trakcie których uczeń bada zależność między dwiema wielkościami fizycznymi.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





