Wiązka zadań
Achilles i żółw
Zadanie
Starożytny filozof grecki Zenon z Elei jest autorem kilku paradoksów (czyli zaskakujących przykładów prowadzących do stwierdzeń sprzecznych ze zdrowym rozsądkiem) dotyczących ruchu. Oto opis jednego z nich:
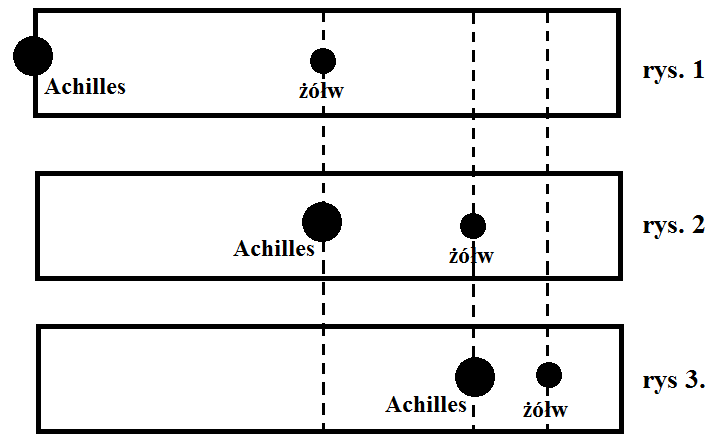
Achilles i żółw stają na linii startu wyścigu na dystans 100 m. Załóżmy, że Achilles potrafi biegać dwa razy szybciej od żółwia. Aby dać szansę żółwiowi jego start umieszczono w połowie dystansu (rys.1). Gdy Achilles dobiegnie do miejsca, z którego startował żółw, żółw przebiegnie25 m(rys 2.). Gdy Achilles przebędzie to 25 m, żółw przebędzie12,5 m (rys. 3), itd., więc Achilles nigdy nie dogoni żółwia.
Zdecyduj, które z poniższych stwierdzeń wynikają z powyższego tekstu, mimo że nie są zgodne z naszą wiedzą o świecie.
| Stwierdzenie | Czy zgodne z tekstem? | |
| 1 | Przed metą Achilles nie dogoni żółwia. | `square` Tak / `square` Nie |
| 2 | Odległość między Achillesem a żółwiem będzie coraz mniejsza. | `square` Tak / `square` Nie |
| 3 | Żółw zawsze będzie w połowie drogi między Achillesem a metą. | `square` Tak / `square` Nie |
Poprawna odpowiedź
1.TAK., 2.TAK., 3.TAK.
Wymaganie ogólne
1 Wykorzystanie wielkości fizycznych do opisu poznanych zjawisk lub rozwiązania prostych zadań obliczeniowych.
4 Posługiwanie się informacjami pochodzącymi z analizy przeczytanych tekstów (w tym popularno-naukowych).
Wymaganie szczegółowe
1.1. Ruch prostoliniowy i siły. Uczeń posługuje się pojęciem prędkości do opisu ruchu/ przelicza jednostki prędkości
Komentarz
Zadanie sprawdza umiejętność wyciągania wniosków z analizowanych tekstów popularnonaukowych.
Paradoksem nazywamy przedstawienie jakiegoś problemu w inny niekonwencjonalny sposób, który prowadzi do zaskakującego efektu, bardzo często sprzecznego z wynikami naukowymi zarówno teoretycznymi jak i doświadczalnymi.
Opisany w zadaniu paradoks, wymyślony przez greckiego filozofa Zenona z Elei dotyczy postrzegania czasu i przestrzeni w kontekście filozoficznym. Droga i czas traktowane są w nim jak wielkości ciągłe. Podlegają dzieleniu na pół kilka razy z rzędu. Jest to problem bardziej matematyczny niż fizyczny. Można dzielić liczby na pół w nieskończoność i otrzymywać za każdym razem o połowę mniejsze wymierne liczby. W wyniku takiego działania otrzymamy nieskończony zbiór liczb będący ciągiem geometrycznym.
Zadanie dotyczy zależności drogi od czasu w ruchu jednostajnym. Droga w tym ruchu jest proporcjonalna do prędkości. Jeśli prędkość jest dwa razy mniejsza (jak to jest w zadaniu), to droga również jest dwa razy mniejsza. Porównując rys 1, 2 i 3 widać, że z czasem odległość między Achillesem i żółwiem zmniejsza się. Tezy zawarte w zadaniu są słuszne dla początkowych etapów biegu jednak wnioski wyciągnięte na ich podstawie odnoszą się do całości biegu. Rzeczywiście, w czasie w którym Achilles przebiegnie połowę drogi, żółw przebiegnie 1/4 tej drogi. A licząc od mety, kiedy Achilles będzie w odległości 1/2 od mety to żółw 1/4 (rys 2) oraz kiedy Achilles będzie w odległości 1/4 to żółw 1/8 (rys 3) itp. Zatem, odległość między żółwiem i Achillesem zmniejsza się, jednak żółw zawsze będzie w połowie odległości od mety w stosunku do Achillesa (prawdziwe stwierdzenia 2 i 3). Achilles nigdy nie dogoni żółwia (prawdziwe stwierdzenie 1).
W badaniu przeprowadzonym wśród uczniów pierwszych klas liceum ogólnokształcącego, całość zadania prawidłowo rozwiązało 31% badanych. Jest to stosunkowo mała grupa, zważywszy na to, że w każdym z trzech punktów trzeba było wybrać jedną z dwóch podanych opcji. Pierwszą część zadania polegającą na rozstrzygnięciu czy Achilles dogoni żółwia poprawnie wybrało 73% uczniów. Również stosunkowo dużo (80%) stwierdziło, że odległość między Achillesem i żółwiem będzie się zmniejszać. Najmniejszy procent prawidłowych odpowiedzi, 56%, zanotowano dla stwierdzenia 3. Jak można było przypuszczać, stwierdzenia 1 i 3 okazały się najtrudniejsze dla uczniów, gdyż to one stały w sprzeczności z doświadczeniem.
Utwór jest chroniony prawem autorskim. Zasady i warunki korzystania z niego określa Regulamin Serwisu Bazy Dobrych Praktyk.
"Masz uwagi do treści? Uważasz, że zawiera błąd? Napisz na bnd@ibe.edu.pl





